Sides Extended !!!
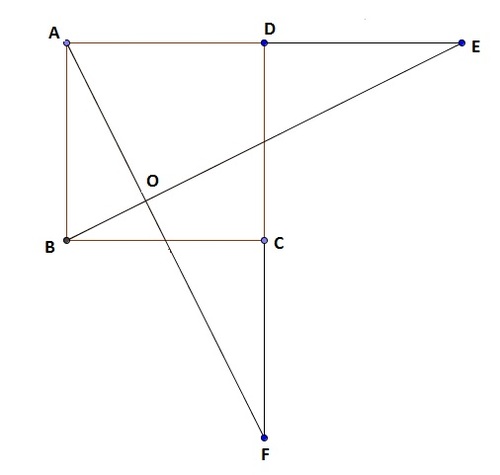 A
B
C
D
is a square. Sides
A
D
and
D
C
are extended to
E
and
F
respectively such that
D
E
=
A
D
and
C
F
=
D
C
.
B
E
and
A
F
intersect at point
O
. If
O
B
O
E
=
n
m
; where
m
and
n
are relatively prime, then find
m
+
n
.
A
B
C
D
is a square. Sides
A
D
and
D
C
are extended to
E
and
F
respectively such that
D
E
=
A
D
and
C
F
=
D
C
.
B
E
and
A
F
intersect at point
O
. If
O
B
O
E
=
n
m
; where
m
and
n
are relatively prime, then find
m
+
n
.
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
10 solutions
 title
title
How a/n = m/a relationship is defined
Log in to reply
Triangle AOB and triangle AOE are similar, so a/nn and m/a is just a relation of sides.
great art :)
how you mak a picture in solution
 Reference image 1
Reference image 1
a : y = 0 b : x = 0 c : y = 1 d : x = 1 e : y = − 2 x + 1 f : y = 2 x A ( 0 , 1 ) B ( 0 , 0 ) C ( 1 , 0 ) D ( 1 , 1 ) E ( 2 , 1 ) F ( 1 , − 1 ) O ( x , y )
I - Discovering O's coordinates:
2 x = 1 − 2 x 2 x + 2 x = 1 2 5 x = 1 x = 5 2 = 0 . 4 y = 2 0 . 4 = − 2 × ( 0 . 4 ) + 1 = 0 . 2 O ( 0 . 4 , 0 . 2 )
II - Discovering E B O E
 Reference Image 2
Reference Image 2
P 1 ( 0 . 4 , 0 ) P 2 ( 2 , 0 . 2 ) ∠ O B P 1 a n d ∠ E O P 2 a r e c o n g r u e n t ∠ B O P 1 a n d ∠ O E P 2 a r e c o n g r u e n t △ B O P 1 a n d △ O E P 2 a r e s i m i l a r
B O O E = B P 1 O P 2 = P 1 O P 2 E = n m
B P 1 O P 2 = 0 . 4 − 0 2 − 0 . 4 = 0 . 4 1 . 6 = 1 4 = n m
m = 4 ; n = 1
III - Summing m and n m + n = 4 + 1 = 5
So, the answer is 5
Notice that triangle AOB and triangle EOA and triangle EAB are similar. Since AB/AE = 1/2 = OB/OA = OA/OE. So OE = 4*OB so the required fraction is 4/1 so the answer is 5.
Yes,exactly the same I did and this the simplest way to solve this . K.K.GARG,India
yes. good job guys
Lets name the intersection point of AF at BC be G. How do you prove the G is the midpoint of line segment BC?
A E O E = A F D F
2 O E = 5 2
O E = 5 4 5
O B = B E − O E
O B = 5 − 5 4 5 = 5 5
O B O E = 1 4
m + n = 4 + 1 = 5
Let ∠ B A F = ∠ A F D = ∠ x and ∠ A O B = y
In △ A O B ,
O B sin B A O = A B sin A O B
⇒ O B sin x = A B sin y _ _ _ (1)
In △ A O E ,
O E sin O A E = 2 A D sin A O E [ A D = D E ]
⇒ O E sin ( 9 0 − x ) = 2 A D sin ( 1 8 0 − y )
⇒ O E cos x = 2 A D sin y _ _ _ (2)
Again in △ A D F ,
tan x = 2 A B A D [ A B = C D ]
Divide ( 1 ) by ( 2 ) .....
tan x O B O E = A B 2 A D
O B O E = tan x × A B 2 A D
O B O E = A D × A B 2 A D × 2 A B
O B O E = 4 = 1 4 = n m
Hence, m + n = 4 + 1 = 5
A quicker approach: ∠ A E O = 9 0 ∘ − ∠ O A E = ∠ O A B . Hence △ A B E ∼ △ A O B ∼ △ A O E . Since A E = 2 A B , we have A O = 2 O B ⟹ O B = A O / 2 and O E = 2 A O . So O E / O B = A O / 2 2 A O = 4
Log in to reply
From the beginning you have considered that AOE = 90° . How?
Log in to reply
This is trivial to prove. Note that △ A B E ≅ △ A D F by SSS congruence theorem. So ∠ A F D = ∠ A E B . Consider △ A O B and △ A B E which has ∠ A B E in common and ∠ O A B = ∠ A F D = ∠ A E B . So △ A O B ∼ △ A B E . Hence ∠ A O B = ∠ B A E = 9 0 ∘ = ∠ A O E .
Yes, that's how I did it. I used similar triangles.
Ruan's answer is similar to mine, but takes a very long workaround once O is found. Here is a shorter version:
Assume the lower left corner of the square is the origin of the Cartesian x-y plane; in other words, it is (0,0).
- B: (0,0)
- A: (0, 1)
- E: (2, 1)
- F: (1, -1)
From these points, it is relatively easy to deduce that the line AF is y = − 2 x + 1 , and the line BE is y = 2 x . These lines intersect at − 2 x + 1 = 2 x 2 5 x = 1 x = 5 2 Plugging this x value into line BE returns y − 5 1
So now we have point O: (\frac{2}[5}, \frac{1}{5}) . Since AEB is a triangle, we can just use the ratio of the y-differences from B to O and from O to E. Thus, O B O E = 5 1 5 4 O B O E = 4 1 And therefore, m + n = 5
It can be seen that Δ A O B and Δ A O E are similar to Δ A B E .
Therefore, O A O E = A B A E = 1 2 .
Similarly, O B O A = A B A E = 1 2 .
Now, O B O E = O A O E × O B O A = 1 2 × 1 2 = 1 4 .
Therefore, m = 4 and n = 1 ; m + n = 5 .
Just look at diagram and its easy :v
Let BE intersect DE at G, AF intersect BC at N. Let sides of square be s.
Draw GH parallel to BC to intersect AB at G and AF at K.
From triangle AFD, NC = s/2. So BN = s/2.
In triangle ABN, H is midpoint.
We can see GK =(1/2)BN = s/4. So KG = s - s/4 =3s/4
IN similar triangles KGO and NBO...>>. GO/OB =KG/BN = (3s/4)/(s/2)
= (3/2) *
BG = GE = BO + GO = (5/2)BO
So...>> OE/BO = (OG + GE)/BO = {..(3/2) * BO..+..(5/2) * BO..}/BO = 8/2 = 4/1 = a/b... a+b = 5
1- let side of square be a. therefore AB = a
2- let AF intersect BC at P
3- notice that OB is the altitude for AOB
4- hence area of AOB = [ .5 * AP *BO ] = [ .5 * AB * BP]
5- AP = a * root5/2 (pythagoras on ABP)......AB = a (side of square)....BP = a/2 (half of side)
6- therefore BO = n = a/root5
7- BE =a* root5
8- therefore m = 4a/root5
9 - therefore m+n = 5
No measurement is given of the side of the square. ..how is the answer 5???