Sierpinski Counter
Probability
Level
3
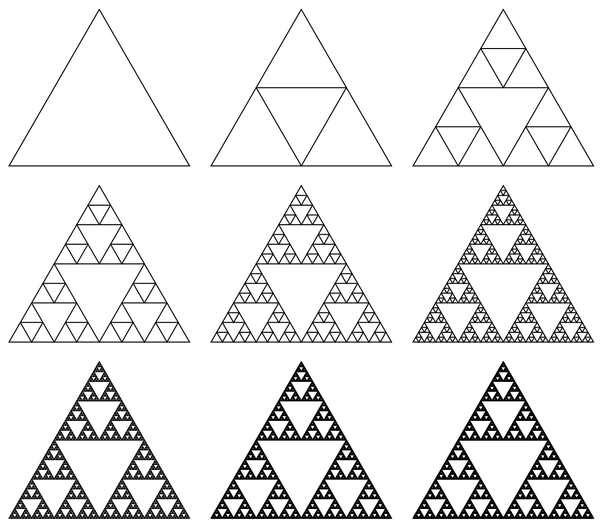
Consider the above image, where a 'Sierpinski triangle' is built iteratively. How many triangles are there in the last iteration shown?
The answer is 13121.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We begin with one triangle, to which we add a smaller triangle in the middle. After this, there are 3 spaces where we can add even smaller triangles, and then 3 2 spaces, and then 3 3 spaces, and so on. Every time we add a new, smaller triangle to the previous iteration, we gain 4 new triangle shapes (look at the upper middle image if this is unclear). Thus, the expression for the number of triangles in a partially-completed Sierpinksi triangle after n such iterations is equal to 1 + ∑ n = 0 n − 1 4 ( 3 n ) (where n = 0 for the first empty triangle). A classic formula for such an exponential sum is ∑ n = 0 n − 1 = 1 − r 1 − r n . Accordingly, our sum becomes 1 + 4 ( − 2 1 − 3 n ) , which cancels down to 2 ( 3 n ) − 1 . The last triangle represents n = 8 , so plugging 8 into our formula yields 2 ( 3 8 ) − 1 = 1 3 1 2 1