Sigma on and on...

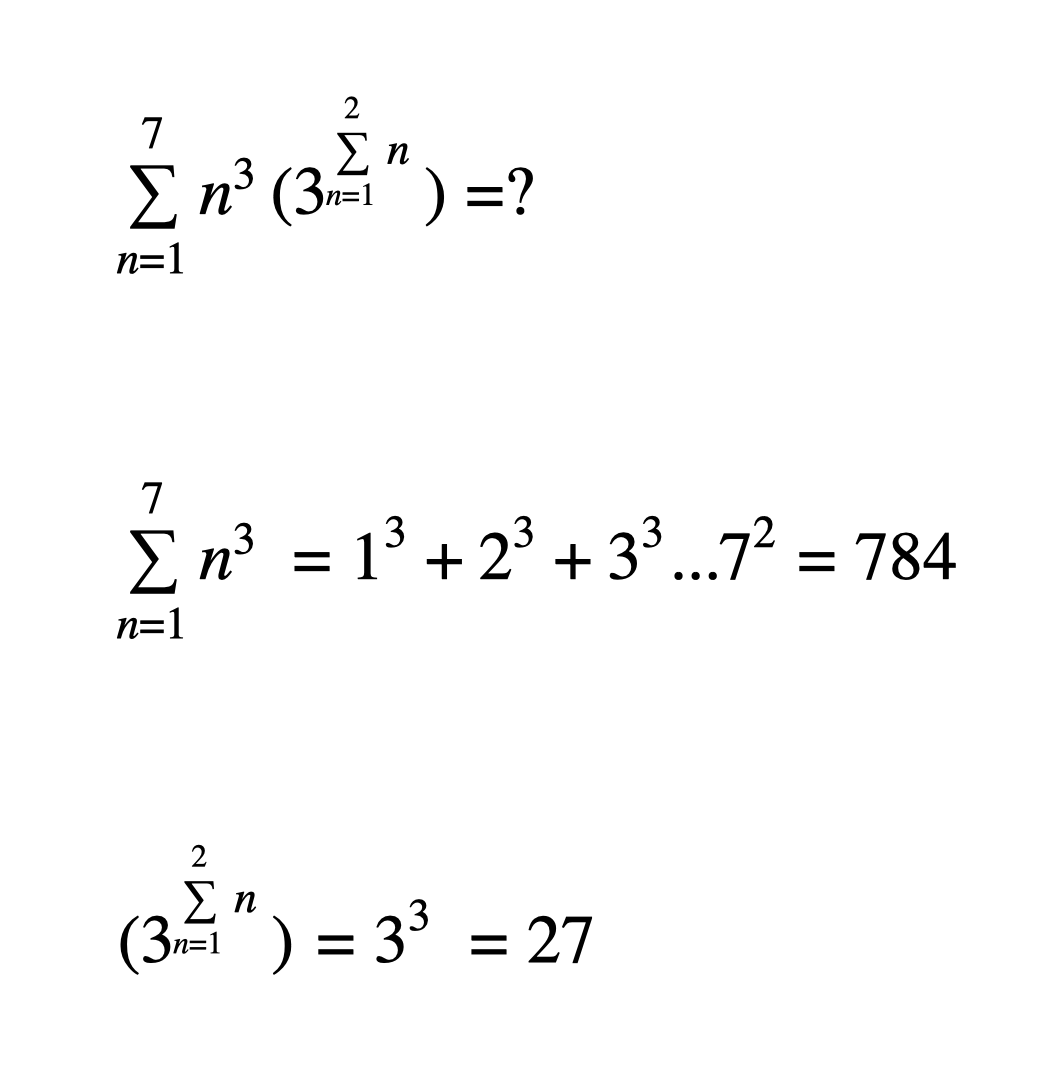
$\displaystyle \sum_{n=1}^{2} n = 1 + 2 = 3$ , and $3^{3} = 27$

$\displaystyle \sum_{n=1}^{7} n^3 \times 27 = 27 \displaystyle \sum_{n=1}^{7} n^3 = 27 (1^3 + 2^3 + 3^3 + 4^3 + 5^3 + 6^3 + 7^3)$

Now, we can just calculate this, but there is a shortcut that I really enjoy. Consider the image below:

Here we have one square with area $1^{2}$ , two squares with area $2^{2}$ , three with area $3^{2}$ , four with area $4^{2}$ , and so on. Or in other words, $1(1^2)$ , $2(2^2)$ , $3(3^2)$ , $4(4^2)$ , etc. This becomes $1^3$ , $2^3$ , $3^3$ , $4^3$ , etc. Every series of even sided squares has an overlap, but this overlap is cancelled out completely by the empty gap. Therefore, we can see that the sum of the cubes fits perfectly in a square every time; numerically, this looks like $1^3 + 2^3 + 3^3 + 4^3 = (1+2+3+4)^2$ , and likewise, following this pattern, $1^3 +2^3 + 3^3 + \cdots + n^3 = (1+2+3+\cdots +n)^2$ . So $(1^3 + 2^3 + 3^3 + 4^3 + 5^3 + 6^3 + 7^3) = (1+2+3+4+5+6+7)^2 = 28^2 = 784$ . Then $784*27=21168$ .

We then multiply 784 by 27 to get 21,168, which is the answer.