Signal transport inside a coaxial cable

Electricity and Magnetism Level 2

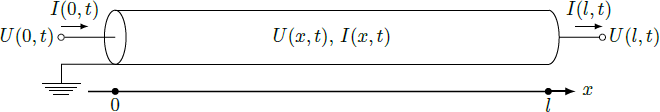
A coxial cable consists of an inner conductor and an outer conductor, which are insulated from each other by a dielectric. While the outer conductor acts as a shield and is earthed, an AC signal is transmitted through the inner conductor. The coax acts both as a capacitor and as an inductance, so that electrical signals propagate only with a certain delay in the cable. In this task we assume for the capacitance and inductance the values $\begin{aligned} C' &= \frac{C}{l} = 3 \cdot 10^{-11} \frac{\text{F}}{\text{m}} \\ L' &= \frac{L}{l} = 1.5 \cdot 10^{-6} \frac{\text{H}}{\text{m}} \end{aligned}$ per meter. What is the speed of electromagnetic waves in the cable in units of vacuum light speed $c_0 \approx 3 \cdot 10^8 \,\text{m}/\text{s}$ ?

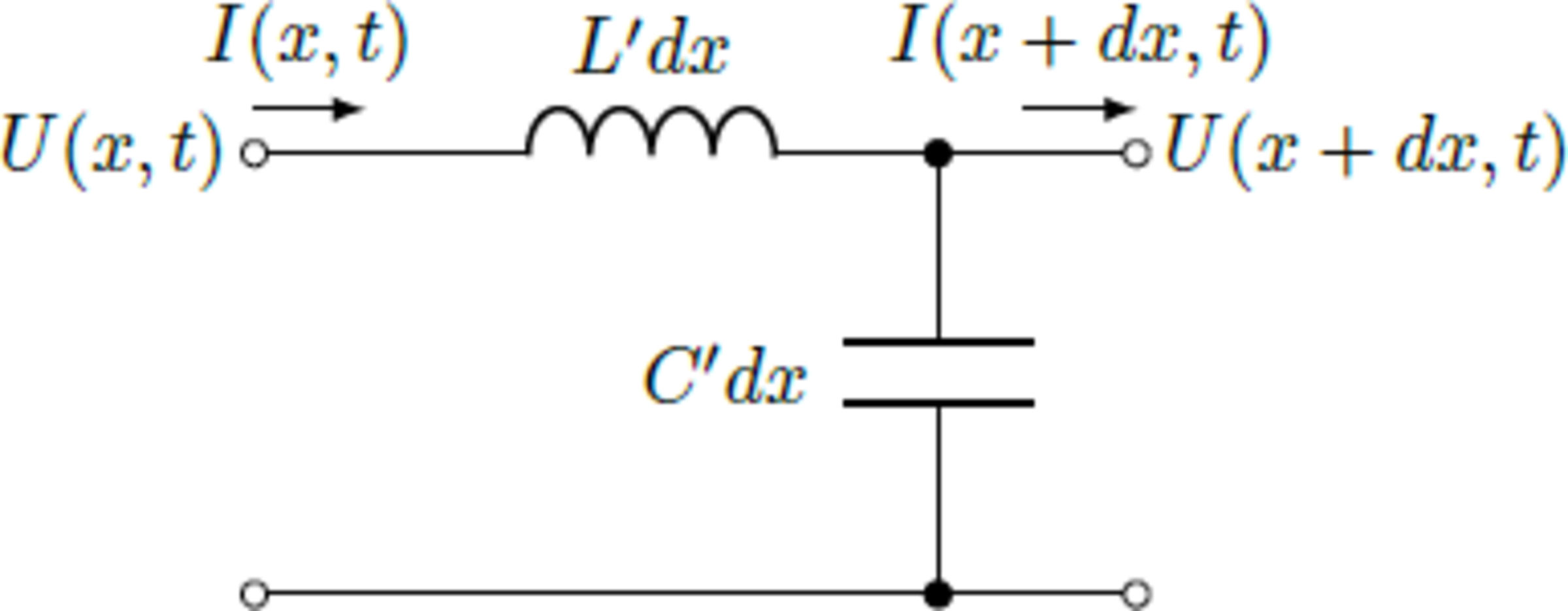
Hint: A cable part of the length dx has a serial inductance $L = L 'dx$ and a parallel capacitance $C = C' dx$ and can be described by the equivalent circuit shown on the right. Use the formulas $\begin{aligned} U_C &= \frac{Q}{C} \\ U_L &= L \frac{dI}{dt} \end{aligned}$ for the voltage drop along the capacitance and the inductance and derive differential equations for the current $I(x,t)$ and the voltage $U(x,t)$ . Show that they satisfy the wave equation $\begin{aligned} \frac{\partial^2 I}{\partial t^2} &= \frac{1}{c^2} \frac{\partial^2 I}{\partial x^2} \\ \frac{\partial^2 U}{\partial t^2} &= \frac{1}{c^2} \frac{\partial^2 U}{\partial x^2} \end{aligned}$ with the phase velocity $c$ .

1 0.25 0 0.5 0.75

1 solution

Steven Chase
Dec 10, 2017

Here are the governing equations for the transmission line:

$\Delta U = -L' \, dx \frac{\partial{I}}{\partial{t}} \\ \Delta I = -C' \, dx \frac{\partial{U}}{\partial{t}} \\ \frac{\Delta U}{dx} = -L' \frac{\partial{I}}{\partial{t}} \\ \frac{\Delta I}{dx} = -C' \frac{\partial{U}}{\partial{t}}$

Taking the limit as $dx$ goes to zero:

$\frac{\partial{U}}{\partial{x}} = -L' \frac{\partial{I}}{\partial{t}} \\ \frac{\partial{I}}{\partial{x}} = -C' \frac{\partial{U}}{\partial{t}}$

Take another spatial partial derivative of the voltage equation and another temporal partial derivative of the current equation:

$\frac{\partial^2{U}}{\partial{x^2}} = -L' \frac{\partial^2{I}}{\partial{x} \partial{t}} \\ \frac{\partial^2{I}}{\partial{x} \partial{t}} = -C' \frac{\partial^2{U}}{\partial{t^2}}$

Equating the mixed-derivative terms:

$\frac{\partial^2{U}}{\partial{x^2}} = L' C' \frac{\partial^2{U}}{\partial{t^2}}$

By inspection, the general solution is of the following form (voltage expression is given, but current is the same):

$U = f(\pm \sqrt{L'C'} x + t)$

This equation represents a traveling wave (either forward-propagating or backward-propagating). To determine the speed of propagation, consider a backward propagating wave:

$U = f( \sqrt{L'C'} x + t)$

Suppose we first look at the wave with space-time coordinates $(x_0,t_0)$

$U_0 = f(\sqrt{L'C'} x_0 + t_0)$

Suppose the time advances to $t_0 + \Delta{t}$ . Where does the same point on the wave reside spatially at this same time? To determine this, find the value of $x$ which keeps the argument the same.

$\sqrt{L'C'} x_0 + t_0 = \sqrt{L'C'} x_1 + t_0 + \Delta{t} \\ \sqrt{L'C'} x_0 = \sqrt{L'C'} x_1 + \Delta{t} \\ x_1 - x_0 = -\frac{\Delta{t}}{\sqrt{L'C'}}$

Thus, the wave propagates backwards. Determine the speed:

$v = \frac{|x_1 - x_0|}{|t_1 - t_0|} = \frac{\frac{\Delta{t}}{\sqrt{L'C'}}}{\Delta{t}} = \frac{1}{\sqrt{L' C'}}$

Plugging in numbers, we see that this particular cable has a propagation speed equal to approximately half the speed of light.

Signal transport inside a coaxial cable

1 solution

0 pending reports