Silly rods

Classical Mechanics Level 3

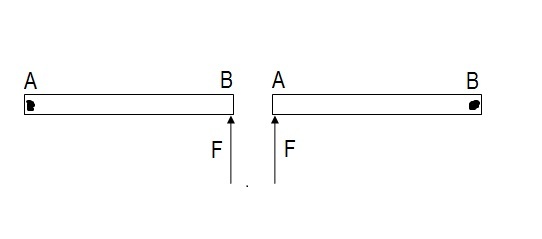
The figure below shows a non uniform metre stick AB having the linear mass density variation λ = λ o x \lambda=\lambda_{o}x where λ o \lambda_{o} is a constant and x x is the distance from end A A , placed on smooth horizontal surface.

In the first experiment, the rod is pivoted at A A and force F F is applied perpendicular to the rod at the other end B B and in the second experiment, the rod is pivoted at B B and the force is applied perpendicular to the rod at the end A A .

If in the first case angular acceleration is α A \alpha_{A} and in the second case it is α B \alpha_{B} then

Refer to my set

α A = α B \alpha_{A}=\alpha_{B} Can not be determined α A < α B \alpha_{A}<\alpha_{B} α A > α B \alpha_{A}>\alpha_{B}

Tanishq Varshney by Tanishq Varshney , 23, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Yash Sharma
Apr 9, 2015

in the first situation...the rod has heavier fraction of its total mass at comparatively larger distance from the center of rotation.........hence i has large moment of inertia.but the second rod has heavier fraction of its total mass near to its center of rotation............hence has less moment of inertia.........since torque is same for both the cases ...the one with less moment of inertia will have greater value of angular acceleration

4 Helpful 0 Interesting 0 Brilliant 0 Confused
Abhishek Sharma
Apr 10, 2015

First Case

I A = m l 2 2 \large {I}_{A}=\frac{m{l}^{2}}{2}

τ A = F l \large {\tau}_{A}=Fl

α = I A τ A \large \alpha=\frac{{I}_{A}}{{\tau}_{A}}

α = 2 F l m l 2 \large \alpha=\frac{2Fl}{m{l}^{2}}

Second Case

I A = m l 2 6 \large {I}_{A}=\frac{m{l}^{2}}{6}

τ A = F l \large {\tau}_{A}=Fl

α = I A τ A \large \alpha=\frac{{I}_{A}}{{\tau}_{A}}

α = 6 F l m l 2 \large \alpha=\frac{6Fl}{m{l}^{2}}

Note: In such a scenario where linear mass density varies linearly with distance from one end, the center of mass is at distance 2 l 3 \frac{2l}{3} from the point from where we are measuring the distance and moment of inertia about center of mass is given by I C M = m l 2 18 {I}_{CM}=\frac{m{l}^{2}}{18} . Derivation of the above statement is trivial and is left as an exercise to the reader.

2 Helpful 0 Interesting 0 Brilliant 0 Confused

Hey, can you please give the derivation for Moment of Inertia about Center of Mass?

Anandhu Raj - 5 years, 2 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...