Similar Curves

Imgur

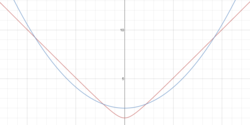
We can draw a rough graph of $y=ax^2+b$ , $y=\sqrt{x^2+1}$ , and their difference, $y=ax^2+b-\sqrt{x^2+1}$ . They are show above, in blue, red, and green respectively.

Obviously to have $q-p$ to be the greatest we must have the green graph take up as much space in the y-range $[-1,1]$ as possible. This means it is tangent to the line $y=-1$ and $y=1$ . It follows that $y=a(0)^2+b-\sqrt{0^2+1}=1$ , so $b=2$ .

Now we must solve for $a$ by using the information that $y=ax^2+2-\sqrt{x^2+1}$ is tangent to $y=-1$ .

We plug in $y=-1$ and rearrange to get $ax^2+3=\sqrt{x^2+1}$ .

Squaring both sides gives $a^2x^4+6ax^2+9=x^2+1$ .

Rearranging gives $a^2x^4+(6a-1)x^2+8=0$

We use the quadratic equation with respect to $x^2$ to obtain $x^2=\dfrac{1-6a\pm \sqrt{4a^2-12a+1}}{2a^2}$ .

Remembering that since the green graph is tangent to $y=-1$ , we must have that the discriminant of this quadratic is zero. Thus, we have $4a^2-12a+1=0$ .

Using the quadratic formula with respect to $a$ , we obtain $a=\dfrac{3}{2}\pm \sqrt{2}$ . However, if $a=\dfrac{3}{2}+\sqrt{2}$ , then $x^2$ is negative, thus $x$ is imaginary; bad. Thus, $a=\dfrac{3}{2}-\sqrt{2}$ .

We have figured out that the blue graph's equation is $y=\left(\dfrac{3}{2}-\sqrt{2}\right)x^2+2$ . The green graph's equation is then $y=\left(\dfrac{3}{2}-\sqrt{2}\right)x^2+2-\sqrt{x^2+1}$ . We now must find the points of intersection of this graph and $y=1$ to determine the values of $p$ and $q$ .

Setting $y=1$ and simplifying, we get $\left(\dfrac{3}{2}-\sqrt{2}\right)x^2+1=\sqrt{x^2+1}$ .

Squaring both sides and subtracting $1$ , we have $\left(\dfrac{3}{2}-\sqrt{2}\right)^2x^4+(3-2\sqrt{2})x^2=x^2$ .

Dividing both sides by $x^2$ (allowed because $x=0$ is not the root we want) we get $\left(\dfrac{3}{2}-\sqrt{2}\right)^2x^2+3-2\sqrt{2}=1$ .

Simplifying: $\left(\dfrac{17}{4}-3\sqrt{2}\right)x^2=2\sqrt{2}-2$ .

Isolating $x^2$ we have $x^2=\dfrac{2\sqrt{2}-2}{\dfrac{17}{4}-3\sqrt{2}}$

Rationalizing, we get $x^2=56+40\sqrt{2}$

Taking the square root and simplifying, we finally get that $q=2\sqrt{14+10\sqrt{2}}$ . Also, $p=-2\sqrt{14+10\sqrt{2}}$ .

Thus, we have that $q-p=\boxed{4\sqrt{14+10\sqrt{2}}}$ , and so our answer is $4+14+10+2=\boxed{30}$ . $\Box$