Similar Pentagon Areas Part 2
Let a pentasquish be a pentagon with the following properties:
- Two non-adjacent right angles
- All sides congruent
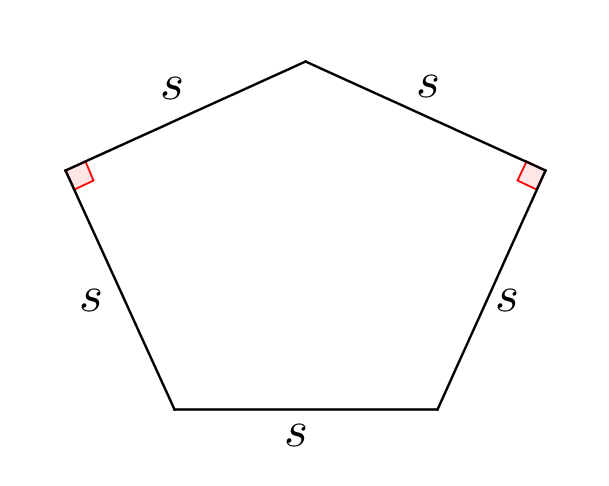
If the area of a pentasquish is , where is the length of one of the sides, and , , and are positive integers with square-free, find .
The answer is 12.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.

A pentasquish consists of two 4 5 − 4 5 − 9 0 triangles with an isosceles triangle between them:
The Pythagorean Theorem can be used to find the height of the isosceles triangle:
h 2 + ( 2 s ) 2 = ( s 2 ) 2
Solving this yields h = 2 s 7
The area of this isosceles triangle is 2 1 × s × 2 s 7 = 4 s 2 7
The two 4 5 − 4 5 − 9 0 triangles together have an area of s 2 .
Thus, the area of the pentasquish is ( 1 + 4 7 ) s 2
a = 1 , b = 7 , and c = 4 , and so a + b + c = 1 2 .