Similar Tangent Ellipses
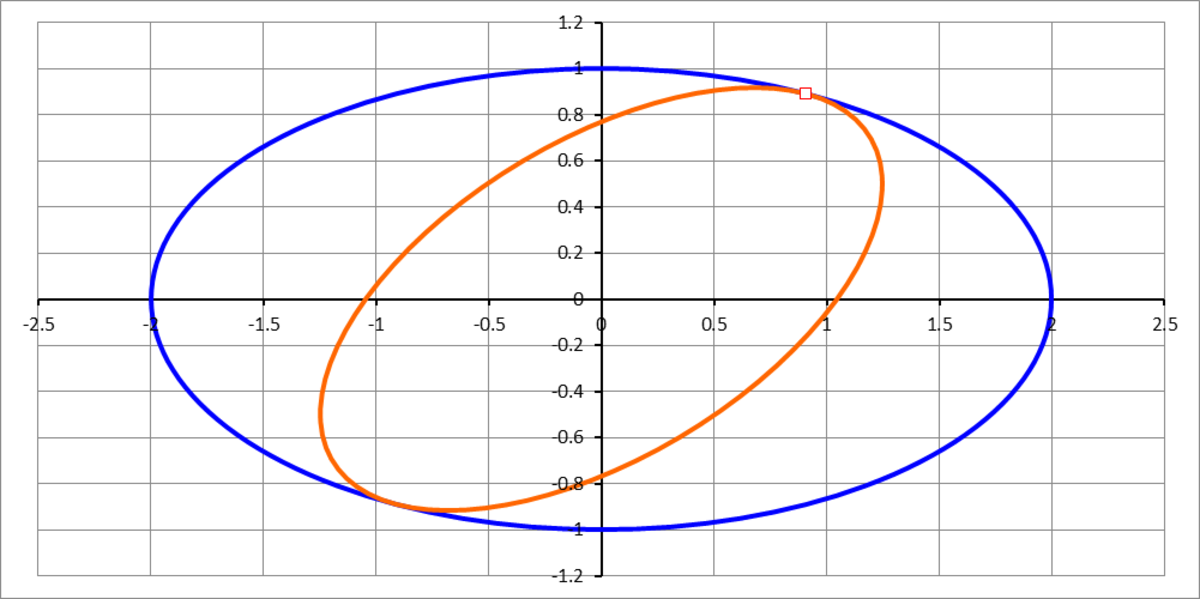
An ellipse (blue) has a semi-major axis of length 2 and a semi-minor axis of length 1. A copy of this ellipse (orange) is rotated and uniformly scaled such that it is similar to the original ellipse, that is, has the same major axis to minor axis ratio. If the angle between the two semi-major axes of the two ellipses is , and the scaled and rotated ellipse is tangent to and inside the original ellipse, then what is the scale factor ? That is, what is the ratio of semi-major axis of the smaller ellipse to the semi-major axis of the larger ellipse ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The equation of the original ellipse is
a 2 x 2 + b 2 y 2 = 1
which can be written compactly as
r T D r = 1
where r = [ x , y ] T , and
D = ⎣ ⎢ ⎡ a 2 1 0 0 b 2 1 ⎦ ⎥ ⎤
Now, for the rotated and scaled ellipse, the equation becomes
s 2 1 r T R D R T r = 1
where s is the scale factor, and
R = [ cos θ sin θ − sin θ cos θ ]
with θ = 3 0 ∘ .
Let vector p be a tangency point between the two ellipses, then p satisfies the following
equations,
p T D p = 1 ............ (1)
s 2 1 p T R D R T p = 1 ............ (2)
In addition, from tangency, the gradient vector of both ellipses are parallel, therefore,
D p = α ( s 2 1 R D R T p ) ............ (3)
Substituting (3) in (1) and comparing with (2), it follows that α = 1 , and hence, from (3), we now have,
( s 2 1 R D R T − D ) p = 0 ............ (4)
Since p is a non-zero vector, then we must have,
∣ ∣ ∣ ∣ s 2 1 R D R T − D ∣ ∣ ∣ ∣ = 0 ............ (5)
The expansion of this 2 × 2 determinant yields a quadratic equation in s 2 1 . Since it is assumed that s > 0 , equation (5) gives two possible values of the scale factor s . These correspond to two possible ellipses, one smaller and one larger than the original ellipse.
Since in this problem, we're interested in the smaller ellipse, we'll take s < 1 .
Performing the computations, yields s = 0 . 6 9 3 .