Similar triangles
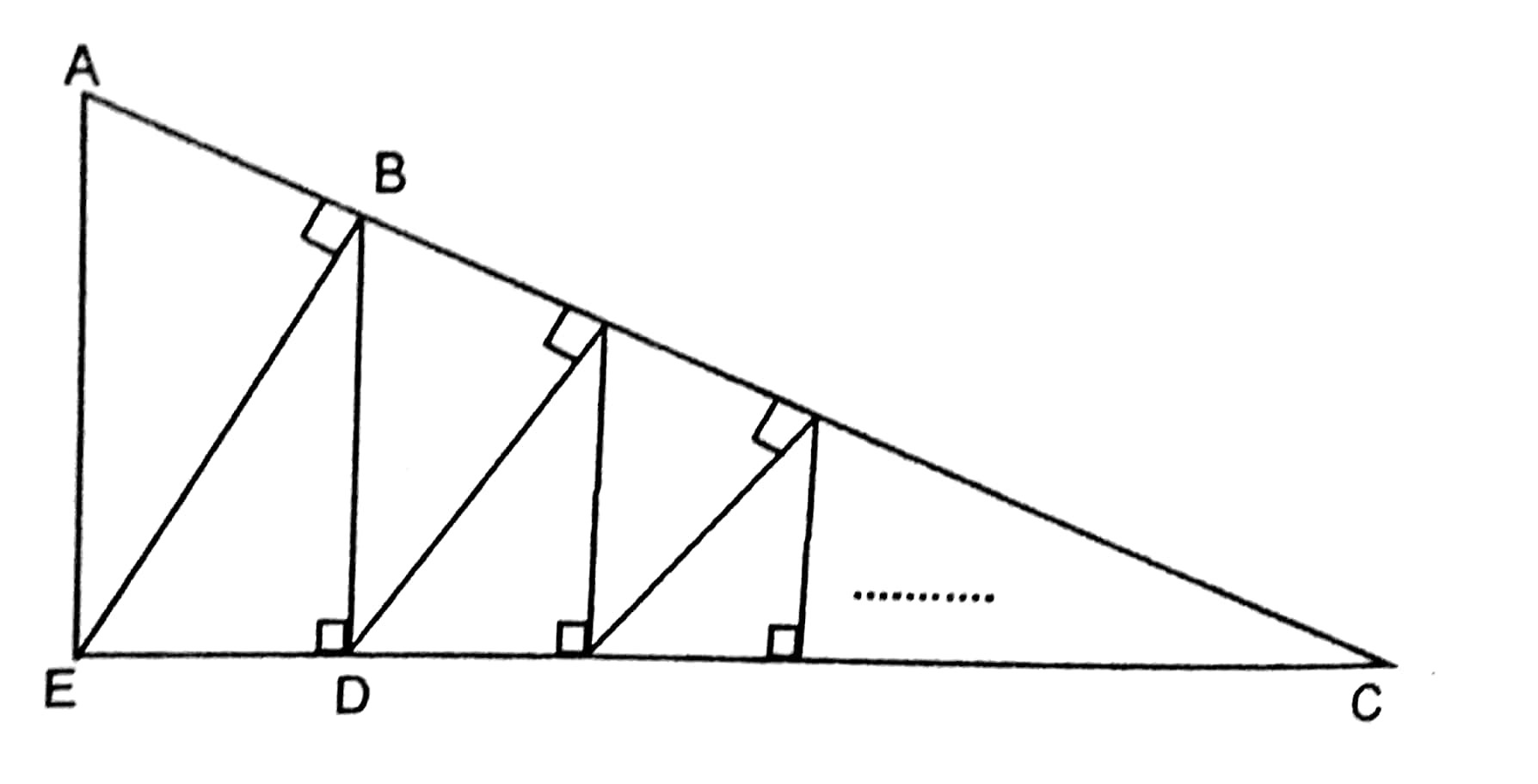
An series of SIMILAR TRIANGLE converges to point C . If A E = 1 6 and E D = 8 . What is the sum of all the vertical segments ( A E + B D + . . . . . ) , such that the length of the last vertical line is an integer.
The answer is 31.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
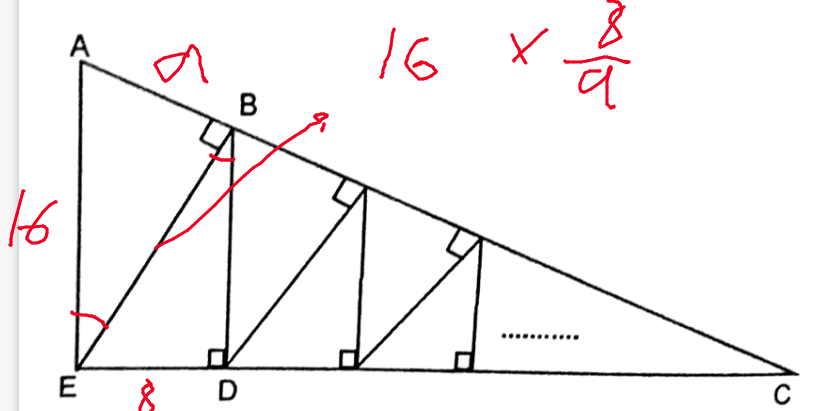by similarity the variables in the eqn above are derived. its just a matter of using pythagoras
a
2
+
(
a
1
2
8
)
2
=
1
6
2
→
a
4
−
2
5
6
a
2
+
1
2
8
2
=
0
→
(
a
2
−
1
2
8
)
2
=
0
→
a
2
=
1
2
8
the ratio is
E
B
=
A
E
a
8
,
B
D
=
E
B
a
8
=
A
E
a
2
6
4
=
2
A
E
. this goes on for all the vertical segments. it follows that what we are look for is
1
6
+
8
+
4
+
2
+
1
=
3
1