Similar triangles?
The
is equal to
. The bisectors and the exterior bisectors of the
angles define the yellow quadrilateral.
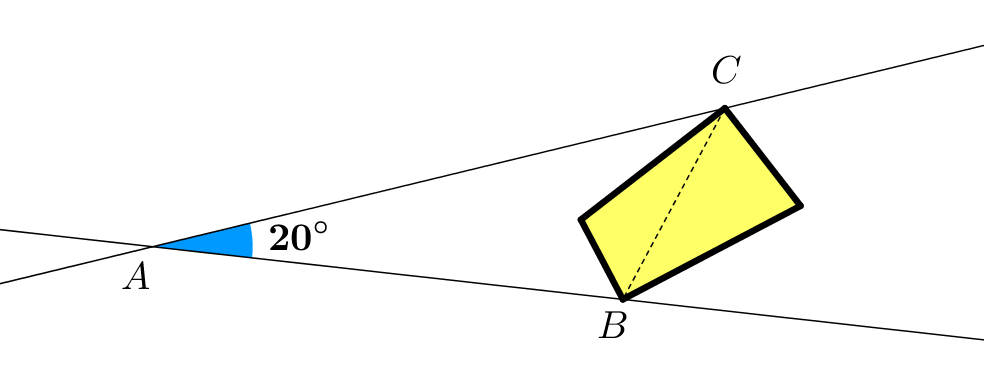
What are the angles of this quadrilateral?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Call the intersection of the interior angle bisectors I and the intersection of the exterior angle bisectors E . Let X be an arbitrary point on A B to the right of B .
Since I B is the angle bisector of ∠ A B C , ∠ I B C = 2 1 ∠ A B C .
Since I E is the angle bisector of ∠ C B X , ∠ C B E = 2 1 ∠ C B X = 2 1 ( 1 8 0 − ∠ A B C ) = 9 0 − 2 1 ∠ A B C .
Thus, ∠ I B E = ∠ I B C + ∠ C B E = 2 1 ∠ A B C + ( 9 0 − 2 1 ∠ A B C ) = 9 0 ∘ . A similar process also shows that ∠ I C E = 9 0 ∘ . This narrows our choices down to either the first or the last one.
Now, we shall find ∠ B I C . Since ∠ I B C = 2 1 ∠ B and ∠ I C B = 2 1 ∠ C , we have
∠ B I C = 1 8 0 − ( ∠ I B C + ∠ I C B ) = 1 8 0 − 2 1 ( ∠ B + ∠ C ) = 1 8 0 − 2 1 ( 1 8 0 − ∠ A ) = 9 0 + 2 1 ∠ A = 9 0 + 2 1 ( 2 0 ) = 1 0 0 ∘ .
Thus, we conclude that B I C E has angles 1 0 0 ∘ , 9 0 ∘ , 9 0 ∘ , 8 0 ∘ .