Similiarity
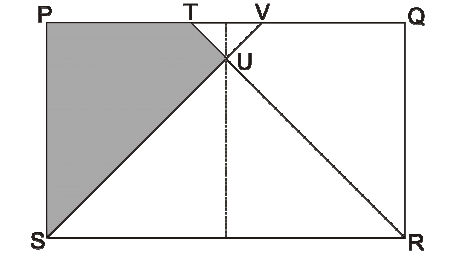 If PQRS is a rectangle:
If PQRS is a rectangle:
PV = QT = PS = 6 and
PQ = SR = 10
What is the value of the shaded area?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
right :)
Can you tell me pls how did the height of TVU came to be 1
perfect.....:)
Hello,
for the area of shaded region, A = (6 x 5 ) - ( 0.5 x 5 x 5 ) - ( 0.5 x 1 x 1) = 30 - 12.5 - 0.5 = 17 unit^(2)
thanks...
we have PV=PS=6.so PSV=(6 6)/2=18.now we to subtract the area of TUV.Here PV=QT=6 &PQ=10,so TV=2.so TUV=(2 1)/2=1.so the shaded area is PTUS=PSV-TUV =18-1 =17(answer)
Solve first the big triangle that can be formed by the shaded area. Add the area of the rectangle above it including a part that is not shaded so that a rectangle can be formed. Subtract the area of the small triangle that was included in the solution of the rectangle above the big triangle.
i using vector. when i knew big triagle whom shader is 0.5x6x6. then i am looking litle triange. and get the areas is 1. so 18-1 is 17
I using vector. when i knew big triagle whom shader is 0.5x6x6. then i am looking litle triange. and get the areas is 1. so 18-1 is 17
We calculate area of triangle PVS that is 1/2 base X heigft + 3 X6 =18 since triangle TUV is issocellous trianle with base 2 and height 1 so area = 1/2 X 2 X1 =1 Subtracting 1 from 18 we get area of shaded portion 18 -1 =17 Ans
K.K.GARG,India
PV=PS=6 Thus ar(PSV) = 18 Also TUV is right angled at U. Also PQ = 10 give VQ=4 anf TV=2 Thus by applying Pythagoras's theorem to triangle TUV, we get, TU=UV=sqrt(2) Thus ar(TUV)=sqrt(2)*sqrt(2)/2 = 1 Thus area of shaded region = 18-1=17
The area is required for the shared region PTUS. First find the area of the rectangle PQRS=10×6=60 Then find the area of triangle QTR=\frac{1}{2}×6×6=18 Next is the area of triangle SUR=\frac{1}{2}×10×5=25 Now the area will be=60-18-25=17
Thanks for the solution, but I wonder how to calculate the length between midpoint of PQ and U, and also the length between the midpoint of SR and U besides assuming that the diagram is drawn to scale ...
Log in to reply
Hey! I didn't consider the scale. We know that PV=PS, So it can form two sides of a square.Let us consider that mid point of RS is A. The three sides of this Square are PV, PS and SA. So SV is the diagonal to our Square. Which means SV makes an angle of 45° with SR. Same is the case with side RU, which also makes 45° with RS. So we can establish that our triangle is right angled. Further, we can bisect SR by drawing a perpendicular through U and this would make it another right angled isosceles triangle. So we can say that SA=AU and then find the area. It is simpler than it sounds!!
yeah, how did you know that the distance between U to PQ .
To answer Jonathon Moey's question: The smallest triangle is an Rt triangle with one side equal to 1 ie. 6-5=1 and base angles of 45 degrees each therefore the distance between U to PQ = 1. Therefore the area of the white part of the shaded triangle is 1/2(2)(1) or 1. Therefore the area of the shaded part is 18-1=17
how do u knw the distance btween pq and u
Log in to reply
Didn't consider distance between PQ and U. I considered distance between RS and U.
since PQ is 10 and PV is 6, VQ is 4 so TV is 2. since TVU = 1x1 and PVS is (6x6)/2, the shaded area will be 18-1 =17