Altered Square
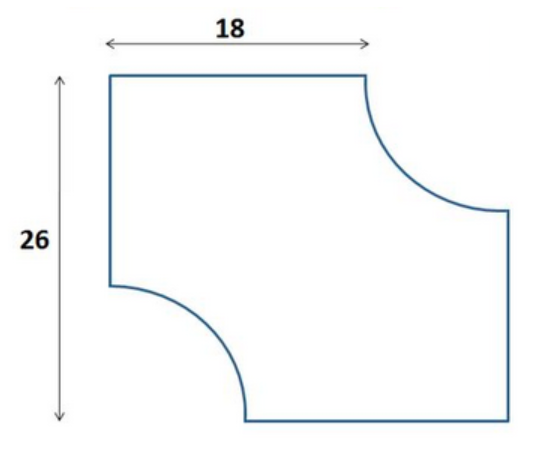 The side length of a square was 26, but now two congruent quarter circles have been cut out, as seen above.
The side length of a square was 26, but now two congruent quarter circles have been cut out, as seen above.
What is the the perimeter of this new shape?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
I don't understand where did the 32 comes from.. Plz can you explain...
Radius of circle = 26 -18 = 8
2 quarter circle's circumference = 2 × π × 8 × 2 1 = 8 π
Perimeter = 1 8 × 4 + 8 π .
The radius of the circle=26-18=8.So the arc of the quarter circles is=(2* pi* r)/4=(pi * r)/2=3.1416 * 8)/2=12.5664.There are two of it so 2 *12.5664=25.1328.Now every straight line is 18,so 4 of them makes the summation (4 *18)=72.So the perimeter of the shape=25.1328+72=97.1328=97.133
how the radius of circle is 8..?which concept ur using by subtracting 26-18 to get the radius
Log in to reply
We know both side are equal because the question states the shape is a square. So subtracting the the long side (26) that includes the radius of the circle and the short side (18) not including the radius of the circle will give the radius of the circle.
As u know side of the square is 26. And all the side of square is equal than if u subtract 18 from 26 you will get radius of the circle
tanA+sinA=P,tanA-sinA=Q than proove-
Is there a flaw in this question or is it me? Yes, you can figure out the radius of 8 for one circle because we know the sides of the square (the smaller side to equal total of the larger.) However, how can you automatically assume the other circle has the same radius by subtracting the same radius; only because of the appearance of drawn similarly? Seems like too far a leap that doesn't fit my logic of presumptions. Nothing indicates that the two quarter circles are of the same radius, diameter, circumference or area, any of which would allow one to a certain deduction.
Log in to reply
It says congruent quarter circles so yes...it does state that they would have the same radius. You can't have two circles with different r's and quarter them to obtain two congruent pieces.
As said there are 2 quarter circles in the square.
Radius of circles would be 26 - 18 = 8.
As it is quarter circle there will be angle of 90 degree.
Hence arc length will be as follows.
arc = (θ × π/180) × r = 90 * π/180 * 8 = 12.56637
Perimeter will be 18 + 18 + 18 + 18 + 12.56637 + 12.56637 = 97.13274.
finding arc length is the main part of this......degree to radian and then l/r = θ rad....yeah.
Y u have written 3 Times the no.12.56637 At last!creating confusion! Dumbo!
Log in to reply
My bad... changed it....
hahahahahah
It is actually a square of each side 26. after cutting its 2 corners in quarter circular shape of radios 8 (26-18=8=r). we get the length of the circular path is (1/4) (2πr) => (1/2) πr ; and the sum of the length of the circular paths is (1/2) πr + (1/2) πr = πr = π* 8 . now the straight lines are of 18, and there four straight lines so its total length is 4* 18=72 and the total length or the perimeter of the shape is 72+π* 8= 97.133
the radius of all the quarter circles is 8/2=4.Now find the perimeter of each as 4*pi/2=2pi.As there are 4 equal quarter circles and 4 sides of 26-8=18. calculate peri. by 4(2pi+18)=97.133
From giveen details,radius of circle is 8. Perimeter full circle is 2 piX8 for two quarter circles it will be 25 .33.for rest of square prtion it is 4 X18 =72. adding all above perimeter of the diagram is 97.33 Ans. K.K.GARG,India
Radius of circle(r) = 26 - 18 = 8
Perimeter of 2 quarter circle (p)= 2 x (1/4) x 2 x pi x r = 8xpi
Perimeter of the shape = 18x4 + p= 97.133
how the radius of circle is 8,,why ur subtracting 26-18 ?
Log in to reply
OK the length of a square is 26... but only 18 was occupied... so that means 8 was occupied by the circle.. and if you gonna draw the whole circle the radius would be 8.. 26 -18 we left 8 which is the half of the circle..
The original perimeter of the square was 4 ⋅ 2 6 = 1 0 4 . Let's see how it has changed.
Four segments of length 2 6 − 1 8 = 8 have been removed, for a total of 32 units removed. On the other hand, 2 quarter-circle arcs have been added. Since the circumference of an entire circle with radius 8 is 2 ⋅ 8 ⋅ π = 1 6 π , 2 quarter-circles will have length 8 π .
Thus, the perimeter is original square 1 0 4 − parts of square missing 3 2 + new curved length 8 π = 7 2 + 8 π .