Reverse Pascal Triangle
 Every brick in this pyramid contains a number that is the sum of the two numbers in the two bricks below it. What is the value of
B
?
Every brick in this pyramid contains a number that is the sum of the two numbers in the two bricks below it. What is the value of
B
?
The answer is 19.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
The format of the bricks will be similar to the Pascal's Triangle
From O and K:
O = A + 4B + 6C + 4D + E
K = B + 2C + D
Substituting given values we can get :
382 = 4B + 3D
121 = B + D
Given those two equations we get B = 19, D = 102
Writing the top layer in terms of the bottom layer:
978 = A + 4B + 6C + 4D + E
978 = A + B + 3(B + 2C + D) + (D + E)
978 = A + B + 3K + I
978 = 137 + B + (3x225) + 147
Therefore, B = 978 - 959
B = 19
So the way to do this is to take B as x , and find all the other boxes in terms of x and hope for your answer to come soon,
B = x
First of all, F = 1 3 7 + x
G = 5 2 + x
J = 1 8 9 + 2 x
M = 4 1 4 + 2 x
And then, K = G + H ⇒ H = 1 7 3 − x
L = 3 2 0 − x
N = 5 4 5 − x
And finally. M + N = O ⇒ x = 1 9
You can see there is a pattern of Pascal Triangle in this question.
@Owen R This was a fun question!
M + N = 978 = J + L + 2(225)
J + L = 528 ............................... (1)
G + H = 225 ..............................(2)
J + L + 225 = 2(G + H) + F + 147 .......................(3)
From (1), (2) and (3)
F = 156
F = 137 + B
B = 19
G + H = 225, B - D = G - H, SINCE (D = 140 - 2B) AND (H = 225 - G), B - (140 - 2B) = G -(225 - G), 3B - 140 = 2G - 225, SINCE (B = G - 52), 3(G - 52) - 140 = 2G - 225 >>> G=71,
THE REST IS HISTORY.
F=137+B
G=52+B
J=189+2B
M=414+2B
O=414+2B+N
H=52+D
L=199+D
N=424+D
O=838+2B+D
2B+D=140
G+H=225
52+B+52+D=225
B+D=121
2B+D=140
B+D=121
--------(-)
B = 19
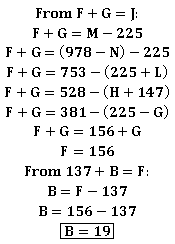
We will use the corresponding lowercase letters to the bricks assigned to them; the top layer is layer 1, the layer below is layer 2, and so on.
Layer 4 :
1 3 7 + b = f
5 2 + b = g
5 2 + d = h
d + e = 1 4 7
Layer 3 :
f + g = j → 1 3 7 + 5 2 + 2 b = j → 1 8 9 + 2 b = j
g + h = 2 2 5 → 5 2 + b + d + 5 2 = 2 2 5 → b + d = 1 2 1
h + 1 4 7 = l → 5 2 + d + 1 4 7 = l → 1 9 9 + d = l
Layer 2 :
j + 2 2 5 = m → 1 8 9 + 2 b + 2 2 5 = m → 4 1 4 + 2 b = m
2 2 5 + l = n → 2 2 5 + 1 9 9 + d = n → 4 2 4 + d = n
Layer 1 :
m + n = 9 7 8 → 2 b + d + 8 3 8 = 9 7 8 → 2 b + d = 1 4 0
Now, we have a system of equations:
{ b + d = 1 2 1 2 b + d = 1 4 0
Substituting the first equation in the second yields:
b + 1 2 1 = 1 4 0 → b = 1 9 , which is the sought answer.