Simple algebra Problem
Given that x and y are positive real such that x + y = 1 , find the value of k such that the maximum value of x 4 y + x y 4 is k 1 .
- This is not an original problem.
- For more problems try my set .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
From the question, we have x + y = 1 ⇒ y = 1 − x . Substituting into the second expression, we get: x 4 y + x y 4 = x 4 ( 1 − x ) + x ( 1 − x ) 4 = − 3 x 4 + 6 x 3 − 4 x 2 + x
Differentiating, we get d x d ( − 3 x 4 + 6 x 3 − 4 x 2 + x ) = − 1 2 x 3 + 1 8 x 2 − 8 x + 1 = 0
Solving the cubic equations, we have found 3 solutions for x : x 1 = 2 1 , x 2 = 6 1 ( 3 − 3 ) , x 3 = 6 1 ( 3 + 3 )
Now, we can sub in each of the respective values of x and we get the answer k = 1 2 .
A bit lengthier but nice solution
Did the same way.
If we use the value of x = 1/2, then y = 1/2 and xy^4 + yx^4 = 2(1/2)^5 = 2/32 = 1/16, so k = 16. See my report. Ed Gray
x 4 y + x y 4 = x y ( x 3 + y 3 ) = x y ( x + y ) ( x 2 + y 2 − x y ) = x y ( 1 ) ( 1 − 2 x y − x y ) = x y − 3 ( x y ) 2 = − 3 ( ( x y ) 2 − 3 1 x y + 3 6 1 ) + 1 2 1 = 1 2 1 − ( x y − 6 1 ) 2 ≤ 1 2 1 Given that x + y = 1 Note that ( x + y ) 2 = x 2 + y 2 + 2 x y Note that ( x y − 6 1 ) 2 ≥ 0
⟹ k = 1 2
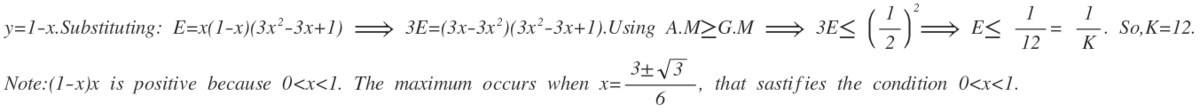
Substituting x = s i n 2 u and y = c o s 2 u .WE will get maximum value equal to 6