Visualize it!
⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ x 2 + y 2 + x y = 1 x 2 + z 2 + x z = 3 z 2 + y 2 + z y = 4
If x , y and z are positive real numbers satisfying the system of equations above, find ( x + y + z ) 2 .
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
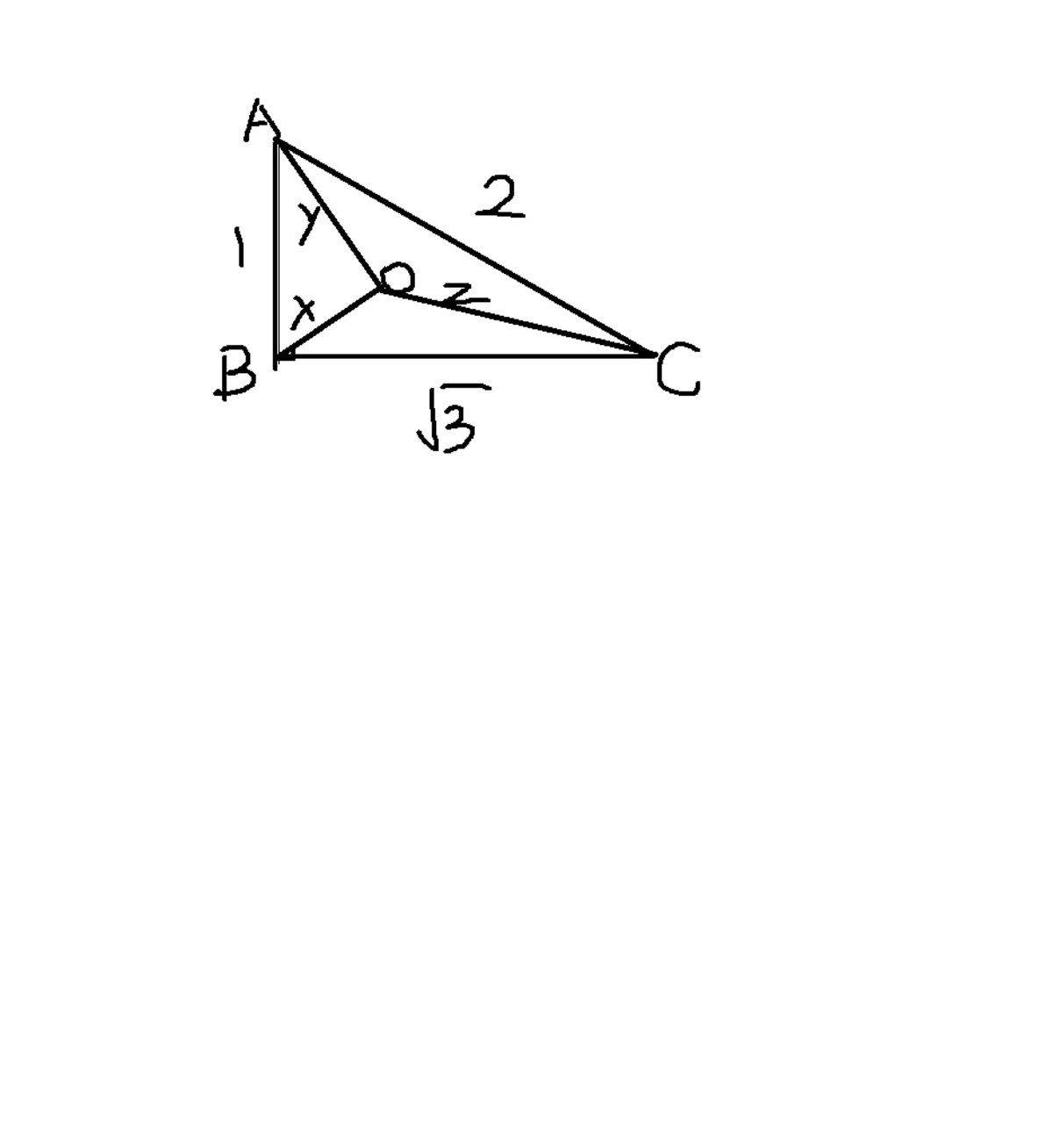

Where did you require cosine formula?
Log in to reply
just use the cosine formula to find out the length of side of the triangle.
this is called a great solution !!
⎩ ⎪ ⎨ ⎪ ⎧ x 2 + y 2 + x y = 1 ( A ) x 2 + z 2 + x z = 3 ( B ) z 2 + y 2 + z y = 4 ( C ) ( B ) − ( A ) a n d ( C − A ) y i e l d : ( z − y ) ( x + y + z ) = 2 ( a ) ( z − x ) ( x + y + z ) = 3 ( b ) D i v i d i n g ( b ) b y ( a ) ( z − y ) ( z − x ) = 3 / 2 w h i c h f u r t h e r s i m p l i f i e s t o z = 3 y − 2 x N o w p l u g g i n g t h i s v a l u e b a c k i n t o ( a ) w e o b t a i n : 4 y 2 − 5 x y + x 2 = 1 ( c ) N o w ( c ) − ( A ) ⟹ 3 y 2 = 6 x y ⟹ y = 2 x N o w z = 6 x − 2 x = 4 x P l u g g i n g i n t o ( b ) x 2 = 7 1 ⟹ x = 7 1 , y = 7 2 , z = 7 4 C h e c k i n g i f o u r s o l u t i o n i s v a l i d , 7 1 + 4 + 2 = 1 ( A ) 7 1 + 1 6 + 4 = 3 ( B ) 7 4 + 1 6 + 8 = 4 ( C ) T h u s ( x + y + z ) 2 = ( 4 9 x 2 ) = 7
Moderator note:
When manipulating equations, we have to check if we introduced extraneous solutions.
For example, there is no solution to x 2 + x = 3 , x 2 = 2 , even though we can subtract the equations to get x = 1 .
As such, you will need to verify that the final value which you calculated is indeed a possible solution to the original system of equations.