charged particle stuck in between two concentric charged cylinders

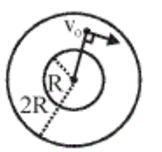
Two long concentric conducting cylinders with cross section as shown in the figure above, have radii $R$ and $2R$ . The inner one carries a charge $\lambda$ per unit length. A particle of mass $m$ and negative charge $-q$ is given velocity $v_0$ perpendicular to axis of cylinders and perpendicular to radial direction at a distance $\dfrac{3R}2$ from the common axis of cylinders. Identify which of the following statements is/are correct.

(A) If the velocity is $v_0 = \sqrt{ \dfrac{q \lambda}{2\pi \epsilon_0 m} }$ , then the particular moves in a circular path.

(B) If the velocity is $v_0 = \sqrt{ \dfrac{q \lambda}{4\pi \epsilon_0 m} }$ , then the particular moves in a circular path.

(C) If the maximum velocity of $v_0$ such that it does not touch the outer cylinder is $v_0 = \sqrt{ \dfrac{16} 7 \cdot \dfrac{q\lambda}{\pi \epsilon_0 m} \ln \left( \dfrac43 \right)}$ .

(D) If the maximum velocity of $v_0$ such that it does not touch the outer cylinder is $v_0 = \sqrt{ \dfrac{q\lambda}{2\pi \epsilon_0 m} \left(1 + 2\ln \left( \dfrac43 \right)\right)}$ .