Simple as ABC!

Geometry Level 3

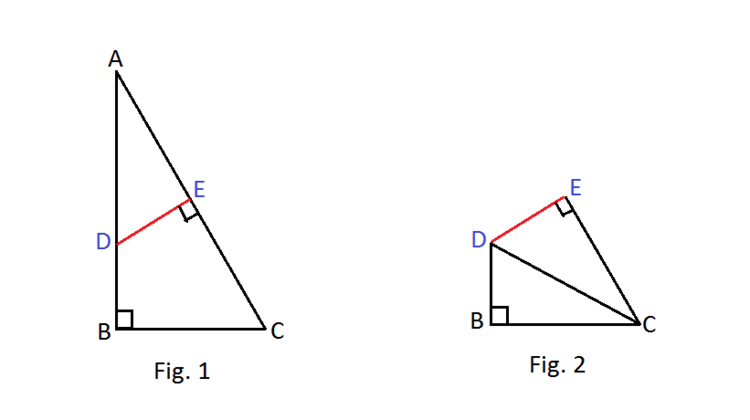A right angled triangle $ABC$ (non-isosceles) was cut from a piece of paper as shown in Fig.1.

A point $E$ was taken at the mid-point of hypotenuse and the figure was folded along $DE$ such that $A$ coincides with $C$ . As a result, two separate right triangles $CBD$ and $CED$ were formed. (Fig. 2)

Take $AC = h$ , $AB = p$ , $BC = b$ .

Which of these answer choices is equal to the ratio $\dfrac{ AC}{CD}$ ?

\frac{p}{h}

\frac{h^{3}}{2p}

\frac{2p}{h^{3}}

\frac{2p}{h}

2 solutions

Brian Charlesworth
Oct 7, 2015

Note first that $\Delta DAE$ and $\Delta DCE$ are congruent right triangles, so

$\dfrac{|AC|}{|CD|} = \dfrac{2*|EC|}{|CD|} = 2*\cos(\angle DAE) = 2*\cos(\angle BAC) = 2*\dfrac{|AB|}{|AC|} = \boxed{\dfrac{2p}{h}}.$

i am totally a idiot

Kaustubh Miglani - 5 years, 8 months ago

Francisco Rodríguez
Oct 7, 2015

Let's $AD=y$ and $AB=x$ , we already know $BC=b$ . Using Pythagoras theorem we get: $y= \sqrt {x^2+b^2}$

Now we know that $x+y=p$ , so we have a 2x2 equation system. We solve it and we get:

$y= \frac {p^2+b^2}{2p}$

If we apply Pythagoras theorem to the original triangle we get $h^2={p^2+b^2}$

So finally,

$\frac {AC}{AD}=\frac {h}{\frac {h^2}{2p}}= \frac {2p}{h}$

Simple as ABC!

2 solutions

0 pending reports