Simple circle problem
Geometry
Level
4
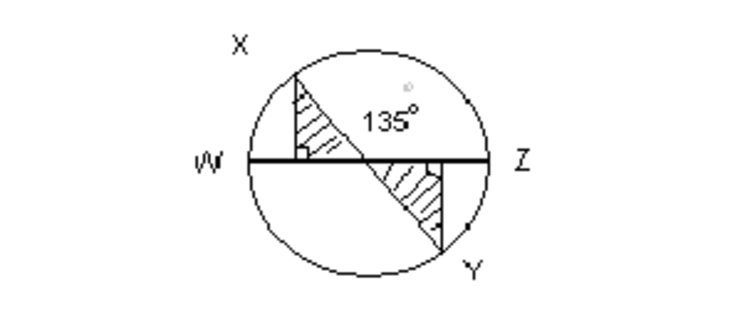
In the figure above, if the chords, WZ and segment XY are diameters of the circle with length 12. then the area of the shaded region?
The answer is 18.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
WELL let us take the centre to be O . Let the perpendicular from X on WZ be A and the perpendicular from Y on WZ be B . THEN the upper triangle is AOX and the lower triangle is BOY .
So as per the question ∠ X O Z = 1 3 5 ∘ .
Which follows that ∠ X O W = 4 5 ∘ . tHIS makes the triangle isoceles .
SO the sides of A O X , A O = A X . Using Pythagorean Theorem We get...
A O 2 + A X 2 = X O 2 . .
⇒ A O 2 + A O 2 = ( 6 ) 2 .
THerefore, A O 2 = 1 8 .
⇒ A r e a O f A O X = 1 / 2 × A O × A O .
⇒ A r e a O f A O X = 1 / 2 × 1 8 .
⇒ A r e a O f A O X = 9 .
⇒ A r e a O f S h a d e d R e g i o n = 2 ⋅ A r e a O f A O X = 1 8 .