Simple Circuit Exercise

Electricity and Magnetism Level 2

A battery of emf $E$ , two capacitor of capacitance $C_1$ and $C_2$ , and a resistor of resistance $R$ are connected as shown in figure.
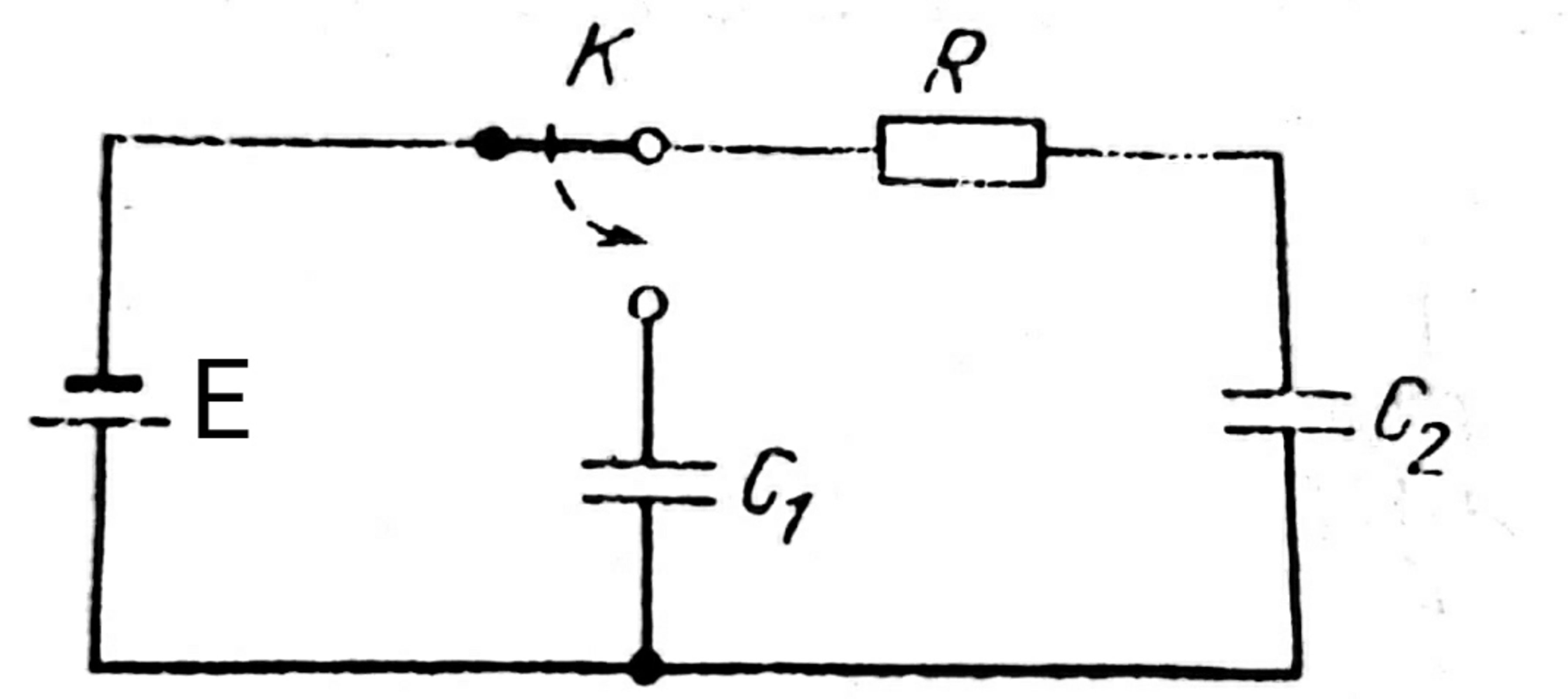
Find the amount of heat $Q$ liberated in the resistor after the key $K$ is switched.

Answer comes in the form of $Q=\frac{E^{\alpha}C_{1}C_{2}}{\beta (C_{1}+C_{2}) }$

Type your answer as $\alpha +\beta=?$

I will be happy if anyone will upgrade this problem.

The answer is 4.

1 solution

A Former Brilliant Member
Jun 9, 2020

Initial energy stored in the capacitor $C_2$ is $\dfrac{1}{2}C_2E^2$ .

Final energy stored in the two capacitors $C_1$ and $C_2$ is

$\dfrac{1}{2}\dfrac {C_2^2}{C_1+C_2}E^2$ .

Hence heat generated in the resistor, being the difference between these two, is

$\dfrac{C_1C_2E^2}{2(C_1+C_2)}$ .

So the required answer is $2+2=\boxed 4$ .

Simple Circuit Exercise

The answer is 4.

1 solution

0 pending reports