A geometry problem by Lee Dongheng
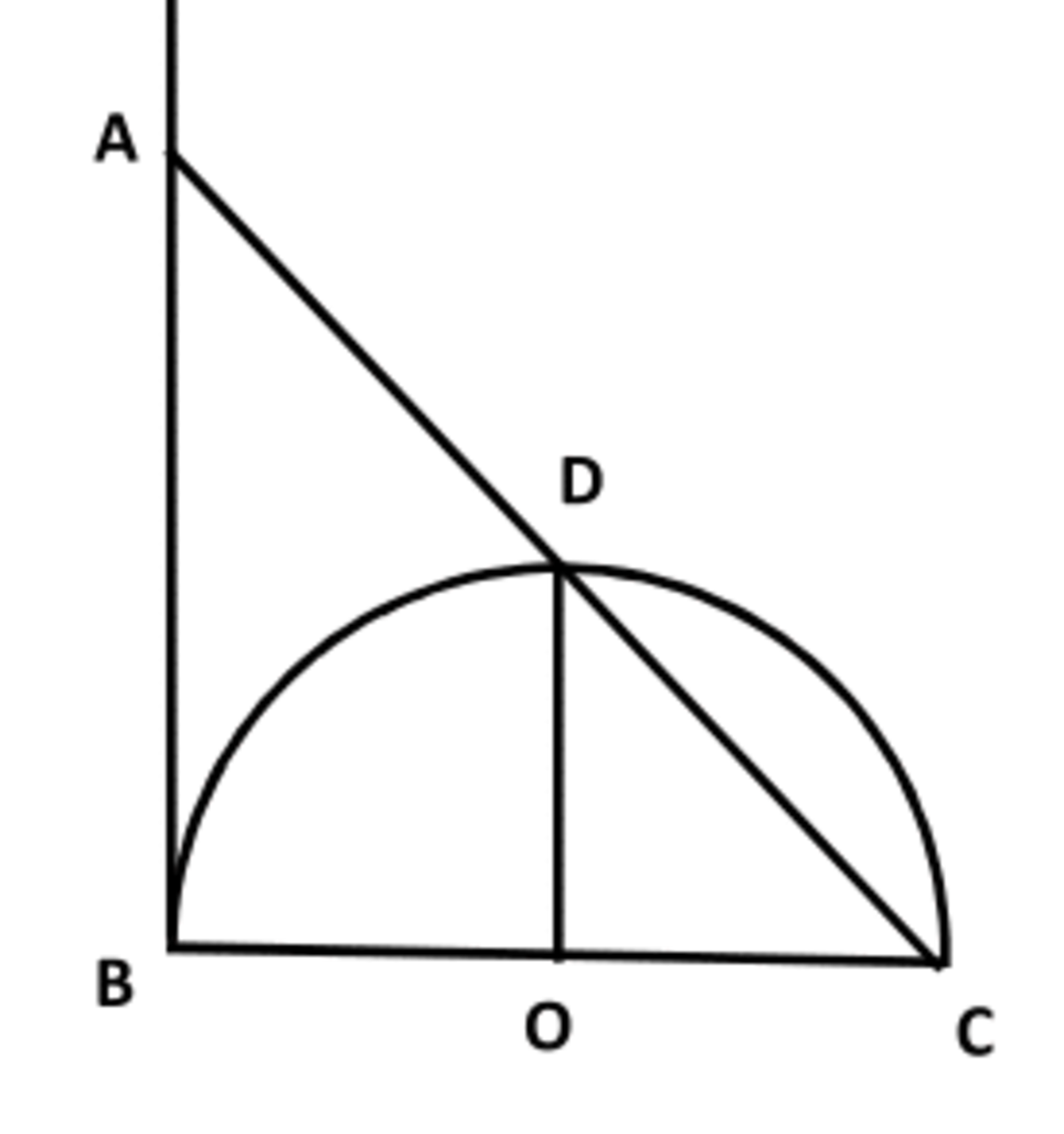
In the diagram below, B C is the diameter and O D is the radius of the semicircle centered at O . If A D = D C , what is sin ∠ O A C ?
Give your answer correct to three decimal places.
The answer is 0.316.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
 O
D
=
O
C
⟹
∡
O
D
C
=
∡
B
A
C
=
4
5
∘
O
D
=
O
C
⟹
∡
O
D
C
=
∡
B
A
C
=
4
5
∘
A B = B C = 2 × B O
∡ B A C = arctan 2 1 ≈ 2 6 . 5 6 5 ∘
∡ O A C = 4 5 ∘ − 2 6 . 5 6 5 ∘ = 1 8 . 4 3 5 ∘
sin O A C = sin ( 1 8 . 4 3 5 ∘ ) = 0 . 3 1 6
We can calculate the answer without using calculator until the final answer, here is a way:
Let O E = a , O E is drawn such that O E ⊥ D C
∴ O C = 2 a , B O = O C = 2 a
∴ A B = 2 2 a
∴ A O = ( 2 2 a ) 2 + ( 2 a ) 2 = 1 0 a
∴ s i n ∠ O A C = A O O E = 1 0 a a = 1 0 1 0 = 0 . 3 1 6