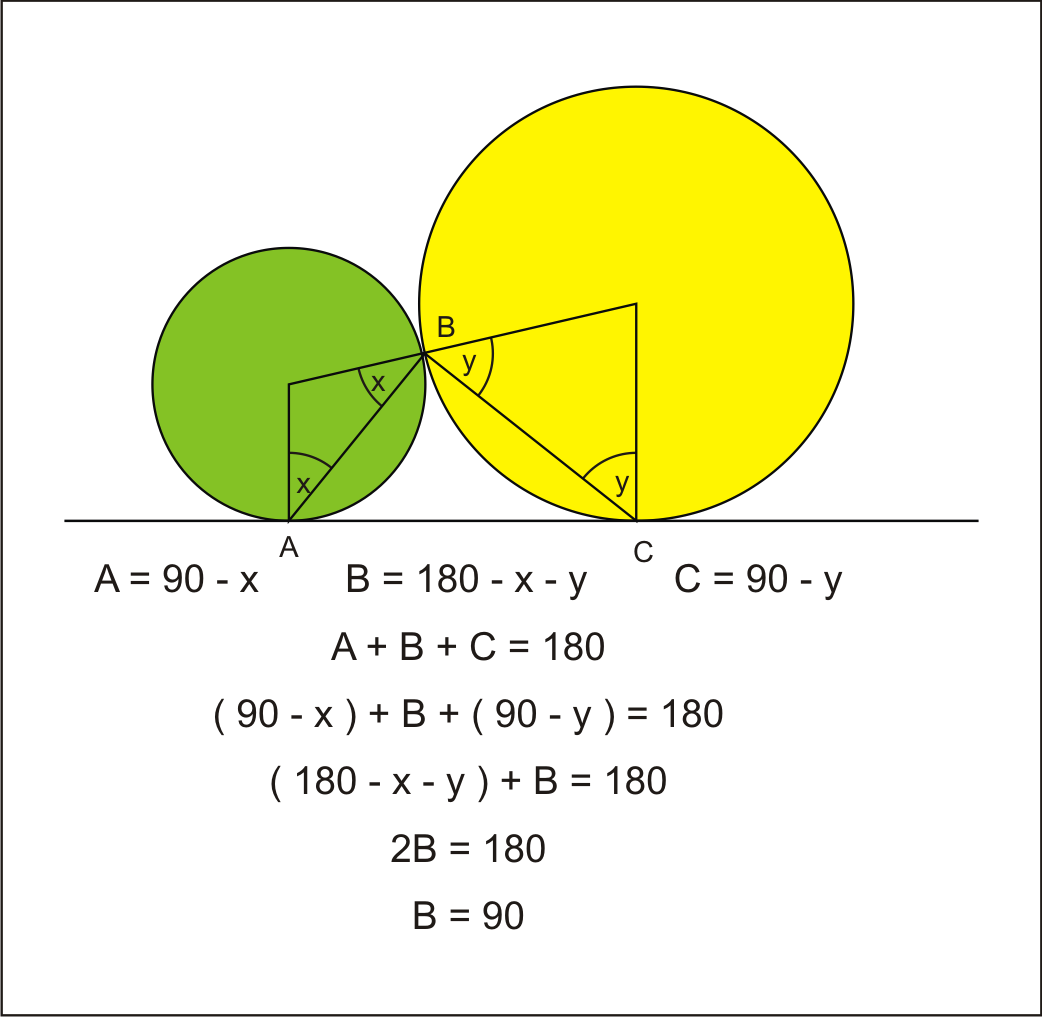
Two Circles and a Triangle
 In the figure
A
C
is a common tangent of two touching circles. If
B
is the touching point of both circles then which is of the following is true about
∠
A
B
C
?
In the figure
A
C
is a common tangent of two touching circles. If
B
is the touching point of both circles then which is of the following is true about
∠
A
B
C
?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Discussions for this problem are now closed
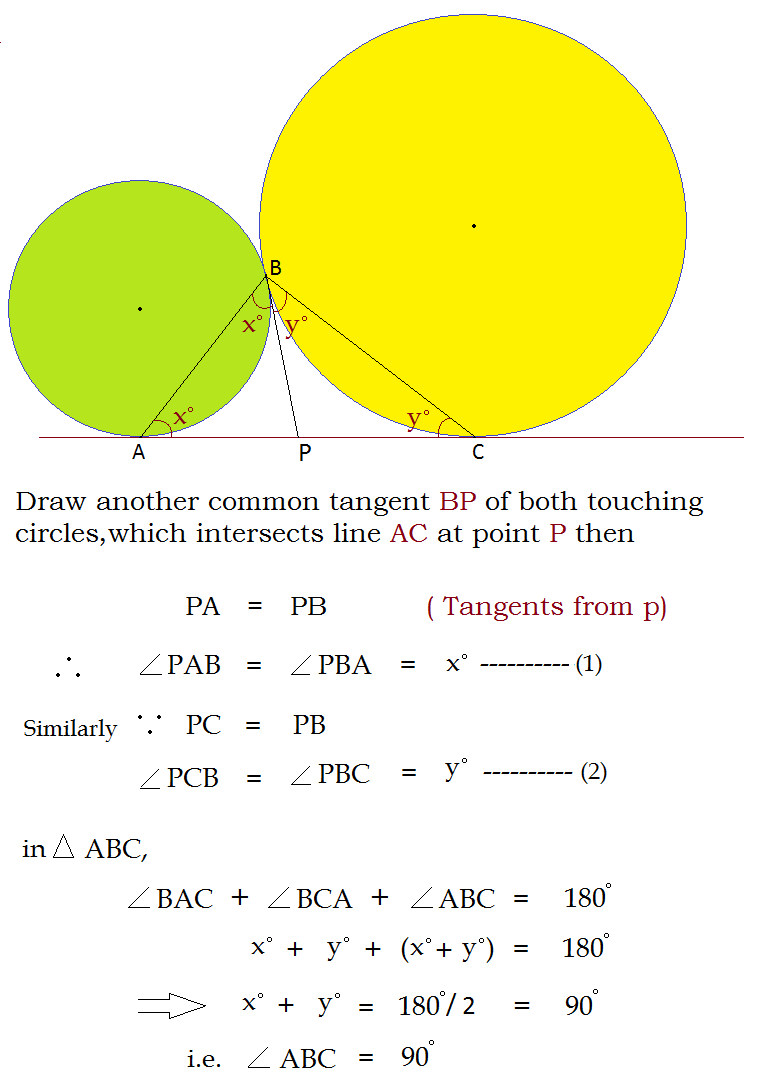
Easy, clear and well explained. Perfect.
Can you please tell me why PA = PB.
Wow,nice solution
Horisadi........ why should the line joining the centre of two circles pass through B?
because point B is also a tangent point of both circle
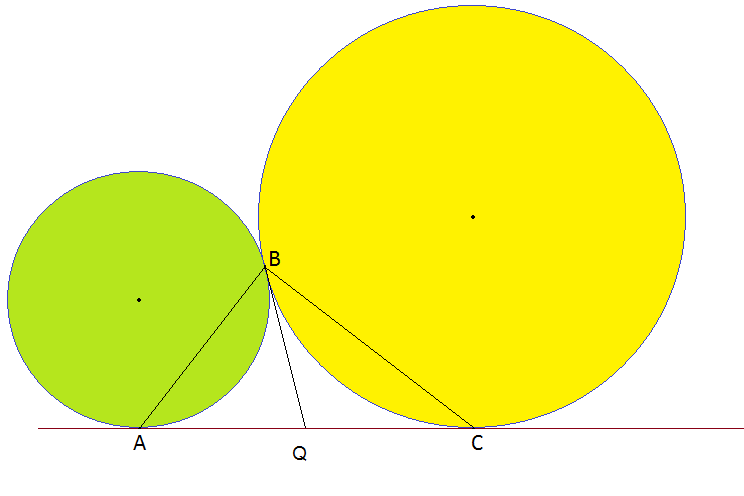
Draw a straight line BQ from B to a point Q on AC. Now, CQ and CA are tangents to the bigger and smaller circle separately.We know that tangents drawn from an external point to a particular circle are equal.Therefore,AQ = BQ and BQ = CQ. So,AQ = CQ. Now, ABC is a triangle in which angle QAB + angle QBA + angle QBC + angle QCB = 180 degree..Since QA = QB and QB = QC,angle QZB = angle QBA and angle QBC = angle QCB.Therefore,2(angle QBA + angle QBC) = 180 degree.Therefore,angle ABC = 90 degree.
Draw a line that goes through B and the centers of both circles. Let that line intersect the smaller circle at P and the bigger one at Q . Also, let line AC extend to the left to point x and to the right to point x . Now angles in a semicircle equal 90 degrees so: ∠ P A B = ∠ B C Q = 9 0 N o w l e t ∠ P A X = a a n d ∠ Q C Y = b . u s i n g a l t e r n a t e s e g m e n t t h e o r e m ∠ Q B C = b a n d ∠ P B A = a ⇒ ∠ A B C = 1 8 0 − ( a + b ) ( 1 ) . By using angle on a straight line = 180 degrees and some angle - chasing gives: ∠ A B C = 1 8 0 − ( 9 0 − a ) − ( 9 0 − b ) = a + b ( 2 ) Now equating (1) and (2): ( a + b ) = 1 8 0 − ( a + b ) ⇒ ( a + b ) = 9 0 . ∴ ∠ A B C = 9 0
Curtis mentioned.....Draw a line that goes through B and the centers of both circles. Pl explain first as to why it would be a straight line.
Let o, O be the center of small, large circles, respectively. Draw in the lines Ao, oO, OC and AoOC make a quadrilateral. We know the sum of the angles of a quadrilateral is 360° Clearly, ∠oAC and ∠OCA are both 90°, and that ∠oBA +∠OBC = 90°, since ∆ oAB and ∆OBC are isosceles. ∴ ∠ABC = 90°
since they don't specify the radii of the circles, we can assume that this is true for all circles. So let the two circles have the same radii. The centres of the circles and A and B form a rectangle, so an angle ABC must be equal to 90 degrees.
You have only proven the case when the two circles have the same radii, but cunning method nonetheless.