Geometry?

From the graph, we have $\cos {2x} = \frac{p}{2q}$ by $\Delta BCD$ .

Then, it is clear that $\angle {ABD} = 180^\circ - 7x$

Using Sine Law, obtain $\frac{p}{\sin {(180^\circ - 7x)}} = \frac{q}{\sin {3x}}$ by $\Delta ABD$ which we can simplify the equation into $\frac{p}{2q} = \frac{\sin {7x}}{2\sin {3x}}$ .

Realize the similarity of this equation and the first equation, we successfully make a pure $x$ equation:

$\cos {2x} = \frac{\sin {7x}}{2\sin {3x}}$

$\sin {7x} = 2\sin {3x} \cos {2x} = \sin {5x} + \sin x$

$\sin x = \sin {7x} - \sin {5x} = 2\cos {6x} \sin x$

Apparently $\sin x \neq 0$ , so

$2\cos {6x} = 1$

$\frac{x}{2} = \boxed{5^\circ}$

A way to solve the problem without using trigonometry is as shown in the diagram .

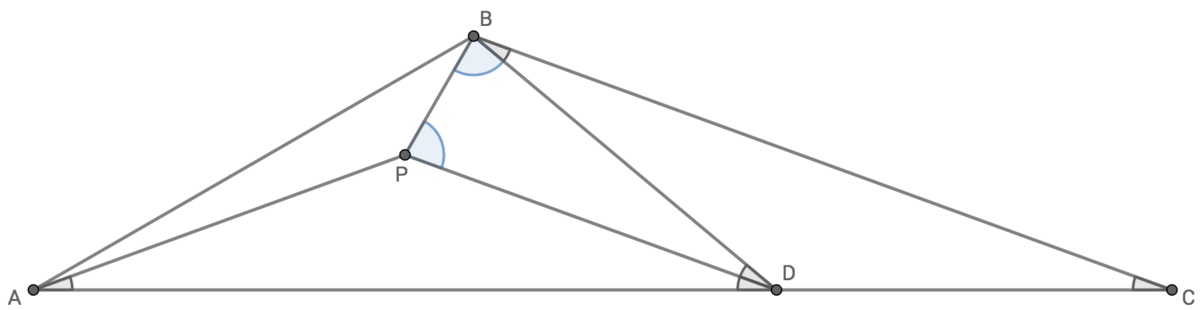
Let $P$ be a point in the interior of $\triangle ABD$ such that $\angle PAD = \angle PDA = 2x^{\circ},$ as shown in the diagram above. Then, since $AD = BC,$ we have $\triangle APD \cong \triangle BDC.$ So, $PD = DB,$ which means that $\triangle DPB$ is isosceles, as indicated in the diagram by the congruent base angles.

We'll find the length of $PB$ using $\triangle DPB.$ First, we can calculate that $\angle ADB = 4x^{\circ}.$ We can further derive $\angle PDB = \angle ADB - \angle ADP = 4x^{\circ} - 2x^{\circ} = 2x^{\circ}.$

Let $X$ be the foot of the perpendicular from $D$ to $PB$ (not shown in the diagram). Also let $a = PD.$ $DX$ is the angle bisector of $\angle PDB,$ so $\angle PDX = x^{\circ},$ giving us $PX = a \sin x^{\circ}.$ By symmetry, $XB = a \sin x^{\circ}$ as well, so $PB = 2a \sin x^{\circ}.$

Now, we shift our focus to $\triangle ABP.$ We find that $\angle BAP = \angle BAD - \angle PAD = 3x^{\circ} - 2x^{\circ} = x^{\circ}$ and

$\begin{aligned} \angle ABP &= \angle ABC - (\angle PBD + \angle DBC) \\ &= 180^{\circ} - (\angle BAC + \angle BCA) - \left ( \dfrac{180^{\circ} - \angle BDP}{2} + \angle DBC \right ) \\ &= 180^{\circ} - (3x^{\circ} + 2x^{\circ}) - \left ( \dfrac{180^{\circ} - 2x^{\circ}}{2} + 2x^{\circ} \right ) \\ &= (90 - 6x)^{\circ}. \end{aligned}$

By the Law of Sines, we have

$\begin{aligned} \dfrac{BP}{\sin \angle BAP} &= \dfrac{AP}{\sin \angle ABP} \\ \dfrac{2a \sin x^{\circ}}{\sin x^{\circ}} &= \dfrac{a}{\sin (90 - 6x)^{\circ}} \\ \sin (90 - 6x)^{\circ} &= \dfrac{1}{2} \\ \cos 6x^{\circ} &= \dfrac{1}{2}. \end{aligned}$

Since $3x$ is one of the degree measures of a triangle, we have $0 < x < 60,$ so the only solution to the above equation is $x = 10.$ Thus, $\dfrac{x}{2} = \dfrac{10}{2} = \boxed{5}.$