Simple Harmonic (5).

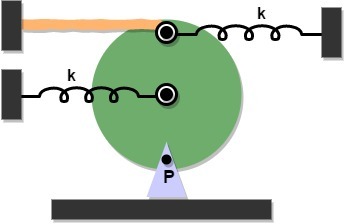
A thin uniform disc of mass $M$ and radius $R$ is hinged at its lowest point and placed in a gravity-free space. It is attached by two identical and ideal springs of force constants $k$ each and a string of cross-sectional area $A$ , length $\ell$ and Young's modulus $Y$ at the positions shown in the figure (centre, top and top). The springs are currently in their natural lengths, the string is unstretched and the whole system is in equilibrium. The disc is given a small angular displacement about the hinge $P$ and allowed to oscillate freely. If the time period of the small oscillations can be expressed as

$T = \pi \left( \sqrt{\dfrac{aM}{bk}} + \sqrt{\dfrac{aM\ell}{bk\ell + cAY}} \right)$

where $(a,b)$ and $(a,c)$ are pairwise coprime positive integers and $a$ and $b$ are both square free. Find $a+b+c$ .