Simple hex
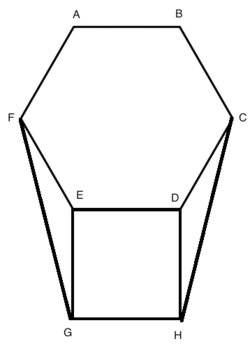Given that ABCDEF is a regular hexagon, and AF = EG, what's the angle measure of
in degrees?
Bonus : Generalize a formula, using the ratio of the relative lengths of EG to AF, to determine the angle measure of . For example (don't enter this as the answer for this problem), if EG is 2 times the length of AF, what will be the new angle measure ?
The answer is 135.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Divide it into angle AFE and EFG- AFE is 120 by (2n-4)90/n for each interior anle of a regular polygon. We know FED is 120, DEG is 90 because it is a square, so sum of angles at a pt is 360 hence FEG must be 150. Since EF an EG are equal, opp angles ar equal too, so by triangle sum property we get 150 + 2EFG is 180 which implies EFG is 15 15 + 120 gives us 135