Constant Integrand?

Let $\alpha = \arctan \left(\dfrac x{1+x^2} \right)$ and $\beta = \arctan \left(\dfrac {1+x^2}x \right)$ $\implies \tan \alpha = \dfrac x{1+x^2}$ and $\tan \beta = \dfrac {1+x^2}x$ . $\implies \tan \alpha = \dfrac 1{\tan \beta} = \cot \beta = \tan \left(\frac \pi 2 - \beta \right)$ , $\implies \alpha = \frac \pi 2 - \beta$ $\implies \alpha + \beta = \frac \pi 2$ for $\alpha > 0$ and $\beta > 0$ . We note that when $x < 0$ , $\alpha, \beta < 0$ , and $\alpha + \beta = - \frac \pi 2$ . Therefore, we have:

$\begin{aligned} I & = \int_{-1}^3 \left( \arctan \left(\dfrac x{1+x^2} \right) + \arctan \left(\dfrac {1+x^2}x \right) \right) \ dx \\ & = \int_{-1}^3 (\alpha + \beta) \ dx \\ & = \int_{-1}^0 (\alpha + \beta) \ dx + \int_0^3 (\alpha + \beta) \ dx \\ & = \int_{-1}^0 - \frac \pi 2 \ dx + \int_0^3 \frac \pi 2 \ dx \\ & = - \frac \pi 2 + \frac {3 \pi}2 \\ & = \pi \end{aligned}$

$\implies A+B = 1+1 = \boxed{2}$

Relevant wiki: Inverse Trigonometric Identities

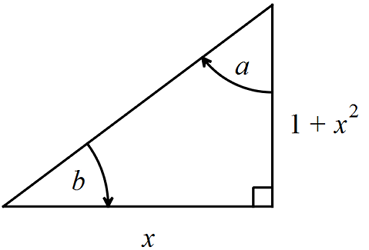
If $x> 0$ , then we can construct a right-angle triangle with base and height of $x$ and $1 + x^2$ .

Looking at the diagram, we have the triangles angle sum of $a + b + \dfrac\pi2 = \pi$ , or equivalently, $a + b = \dfrac\pi 2$ .

Because $\tan a = \dfrac1{1+x^2}$ and $\tan b = \dfrac{1+x^2} x$ , then for $x> 0$ , $\left(\arctan\left(\dfrac x{1+x^2}\right) + \arctan\left(\dfrac {1+x^2}x \right)\right) = a + b = \dfrac\pi2$ .

Since the integrand (call it $g(x)$ ) in question is an odd function , then the integral in question can be expressed as

$\int_{-1}^3 g(x) \, dx = \underbrace{\int_{-1}^1 g(x) \, dx}_{= \; 0} + \int_1^3 g(x) \, dx = 0 + \int_1^3 \dfrac\pi2 \, dx = (3-1)\left (\dfrac\pi2 \right) = \pi \; .$

Hence, $A = 1,B=1\Rightarrow A+B = \boxed2$ .

Note : A common mistake for students to assume is that $\left(\arctan\left(\dfrac x{1+x^2}\right) + \arctan\left(\dfrac {1+x^2}x \right)\right)$ is always equal to $\dfrac\pi2$ .

Let's analyze the function, $y = \tan^{-1} \dfrac 1x$

Substitute $\color{#3D99F6}{\tan \theta = x\\\tan\left(\dfrac \pi 2 - \theta \right) = \dfrac 1x\\\theta = \tan^{-1}x}$

So, $y = \tan^{-1}\left[\tan\left(\dfrac \pi2 - \theta \right)\right]$

Case 1 $x\ge 0$

$\Rightarrow \theta \in\left(0,\dfrac\pi 2\right)\\ \Rightarrow \left(\dfrac \pi 2 - \theta \right) \in \left(0,\dfrac\pi 2\right) \\\Rightarrow \tan^{-1}\left[\tan\left(\dfrac \pi2 - \theta \right) \right]= \left(\dfrac \pi2 - \theta \right)$

Case 2 $x \le 0$

$\Rightarrow \theta \in\left(-\dfrac\pi 2,0\right) \\\Rightarrow \left(\dfrac \pi2 - \theta \right) \in \left(\dfrac\pi 2,\pi\right)$

Remember that for $\phi \in\left(\dfrac\pi 2,\pi\right)$ , $\tan^{-1}\left(\tan \phi\right) = \phi - \pi$

So, $\tan^{-1}\left[\tan\left(\dfrac \pi2 - \theta \right) \right] = \left(\dfrac \pi2 - \theta \right) - \pi = -\dfrac \pi2 - \theta$

$\large \therefore \tan^{-1}\dfrac1x = \begin{cases}\dfrac \pi2 - \tan^{-1}x &\text{for } x>0\\-\dfrac \pi2 - \tan^{-1}x&\text{for } x<0\end{cases}$

---

So our integral, $I = \int_{-1}^3 \tan^{-1}\left(\dfrac x{1+x^2}\right)+\tan^{-1}\left(\dfrac {1+x^2}x \right) \, dx = \int_{-1}^0 -\dfrac \pi 2 \,dx + \int_0^3 \dfrac\pi 2 \, dx = \boxed{\pi}$