Observe the roots, don't expand
∫ 1 7 ( x − 1 ) ( x − 7 ) d x = ?
Bonus : Can you generalize this for ∫ A B ( x − A ) ( x − B ) d x ?
The answer is -36.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Discussions for this problem are now closed
It's just as simple to just integrate and then plug the values in; that wastes a lot of time, however. This is a quick shortcut, and a good one, at that.
we this The solution to this problem is rather simple if you were to use a certain property of definite integrals.
Slightly overengineered solution: make the substitution
x = y + 4 d x = d y ∫ − 3 3 ( y + 3 ) ( y − 3 ) d y 2 ∫ 0 3 ( y + 3 ) ( y − 3 ) d y 2 ∫ 0 3 y 2 − 9 d y 2 ( 3 y 3 − 9 y ) ∣ 0 3 2 ( 9 − 2 7 ) 2 ( − 1 8 ) = − 3 6
Makes it a bit easier to do mentally.
The common way to calculate just to test his theory .
I did it the slow way, expand, ∫ 1 7 ( x 2 − 8 x + 7 ) d x , then use reverse power rule, to integrate, which produces 3 1 ⋅ x 3 − 4 ⋅ x 2 + x ⋅ 7 . After that, substitute in 7 into the expression, and subtract the result of substituting 1 into the expression. ( 3 1 ⋅ 7 3 − 4 ⋅ 7 2 + 7 ⋅ 7 ) − ( 3 1 ⋅ 1 3 − 4 ⋅ 1 2 + 7 ⋅ 1 ) This produces the result − 3 6
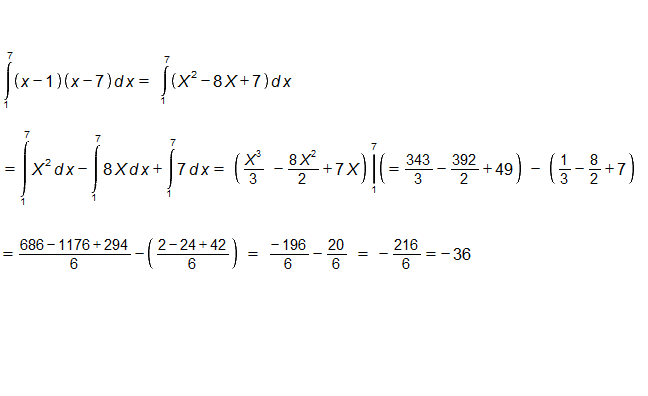
The solution to this problem is rather simple if you were to use a certain property of definite integrals:
∫ α β ( x − α ) ( x − β ) d x = − 6 1 ( β − α ) 3
Here's the proof:
∫ α β ( x − α ) ( x − β ) d x
= ∫ α β [ x 2 − ( α + β ) x + α β ] d x
= [ 3 1 x 3 ] α β − ( α + β ) [ 2 1 x 2 ] α β + α β [ x ] α β
= 3 1 ( β 3 − α 3 ) − 2 1 ( α + β ) ( β 2 − α 2 ) + α β ( β − α )
= 6 1 ( β − α ) [ 2 ( β 2 + α β + α 2 ) − 3 ( β + α ) 2 + 6 α β ]
= 6 1 ( β − α ) ( − β 2 + 2 α β − α 2 )
= − 6 1 ( β − α ) 3
As such, we have
∫ 1 7 ( x 2 − 8 x + 7 ) d x = − 6 1 ( 7 − 1 ) 3 = − 3 6