A geometry problem by VIneEt PaHurKar

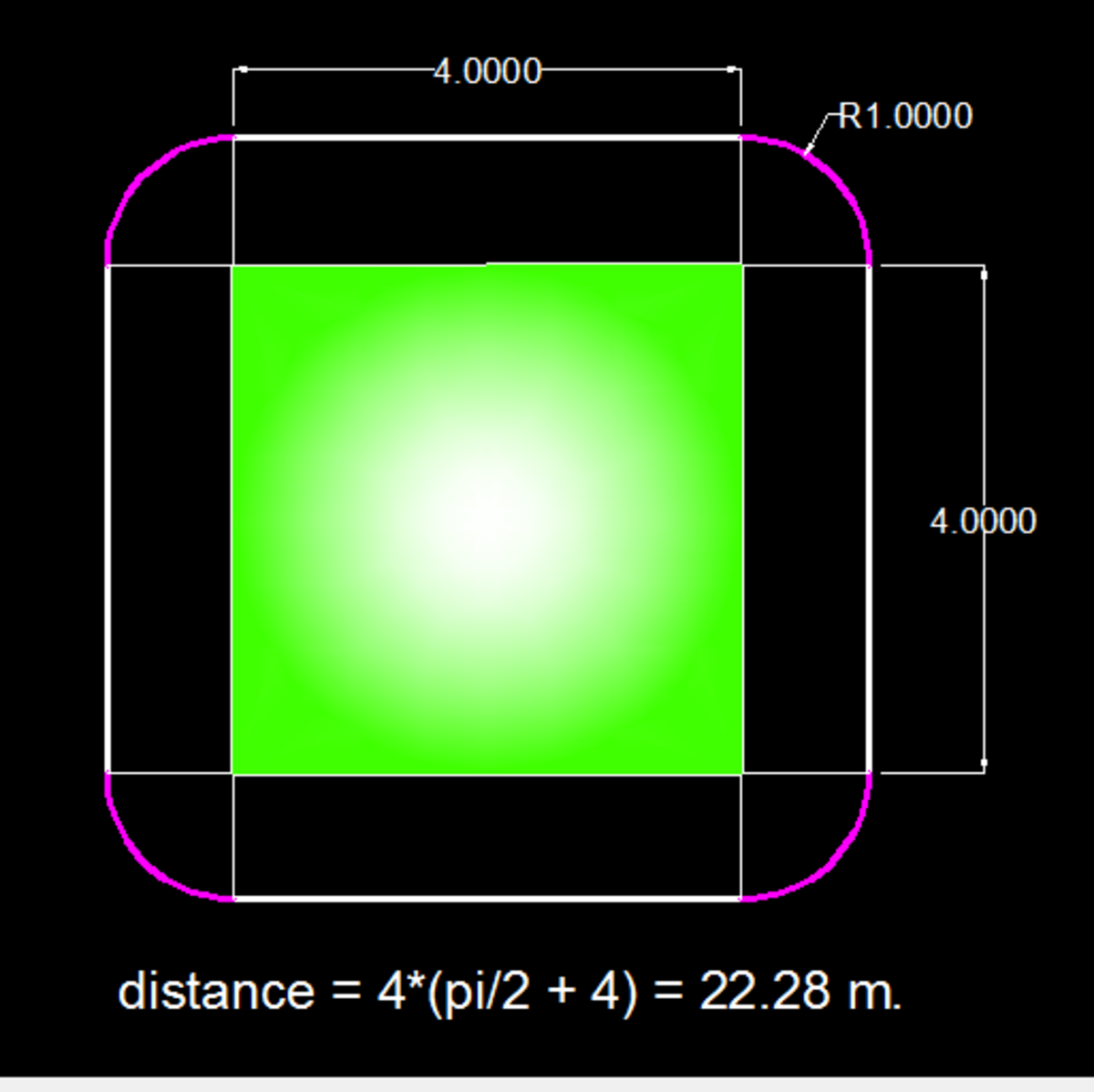
Considering the man's parallel motion from any side of the square;

He travels a distance of $4$ $m$ ; As he passes a side & approaches a vertex,

Now to maintain his $1$ $m$ distance from the square , he must move in a 'curved' path which is actually a $\color{#3D99F6}{quadrant}$ of a circle of radius $1$ $m$ . (Just visualise it)!

$Now$ , collecting everything at one place :-

Distance travelled at one curve(quadrant) $=$

$\dfrac {1}{4}•(2 \pi r)$ $=$ $\dfrac {\pi}{2}$ $m$

Therefore , distance travelled in $4$ such curves $=$ $4 \cdot ( \dfrac {\pi}{2})$ $=$ $2 \pi$ $m$ .

Also, he travels $4$ straight paths each of length $4$ $m$ .

$\mathcal {Summarizing \ everything \ ; Total \ distance \ travelled:}$

$=$ ( $4 \cdot 4$ $+$ $2 \pi$ ) $m$

$=$ $\color{#20A900}{\boxed {22.68 m}}$