Feel a little pull coming through on you
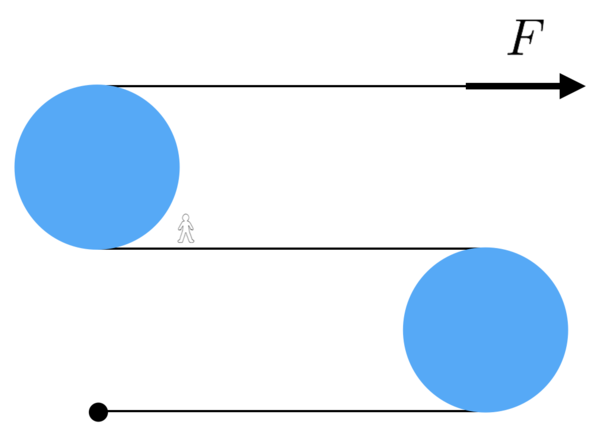
Two identical cylinders of mass and radius lie on a smooth horizontal table with a massless string wrapped around them as shown below. There is sufficient friction between the string and each cylinder such the string does not slip on them. The far end of the string is tied to a particle of mass . If one end of the string is pulled with force , the resultant acceleration of the particle is given by
Find the value of
The answer is 0.043478261.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
This problem takes some careful accounting to develop a coupled set of equations for the tensions, accelerations, and angular accelerations. While obtaining those equations is interesting, solving them is not. So I'll present the full solution for a simpler setup (one cylinder), and simply present the equations for the actual problem. Following the principles from the first obtains the second set of equations without much extension.
The main conceptual obstacle is realizing the consequence of the no-slip condition. Because friction on the string keeps it from slipping with respect to the cylinder, the string loses tension as it goes around the cylinder. In particular, we have T after = T before − I α , where T after is the tension after passing around the cylinder
Suppose we have the same situation as in the diagram, but with only one cylinder. In all of what follows, we adopt the convention that all accelerations are positive.
In other words, since the cylinder moves toward the right,
a
1
is defined to be positive toward the right.
Conversely,
a
2
is defined to be positive toward the left.
We also define the angular acceleration to obey this convention (i.e. so that clockwise is positive).
In all of what follows, we adopt the convention that all accelerations are positive.
In other words, since the cylinder moves toward the right,
a
1
is defined to be positive toward the right.
Conversely,
a
2
is defined to be positive toward the left.
We also define the angular acceleration to obey this convention (i.e. so that clockwise is positive).
First, we write down Newton's second law for the cylinder m a 1 = F + T , and for the mass m a 2 = T . Next, we write down a relation for the angular acceleration of the cylinder under the opposing pull of the two torques I α = F r − T r , where I = 2 1 m r 2 . The final relation reflects the constraint between the acceleration and rotation of the cylinder, and the acceleration of the particle. We are aided in obtaining this relation by the little man standing on the lower string. His acceleration in the lab frame is given by the tangential acceleration of the string relative to the center of the cylinder minus the backward acceleration of the cylinder. This yields a 2 = α r − a 1 . This gives us four equations in four unknowns so that we can proceed with solving the system.
From the torque relation, we have m r α = 2 ( F − T ) . Using the constraint relation, we have m ( a 1 + a 2 ) = 2 ( F − T ) . Subtracting the relation for the acceleration of the cylinder, we have m a 2 = F − 3 T . Substituting the acceleration relation for the particle, we have m a 2 a 2 = F − 3 m a 2 = 4 m F .
By defining variables with similar conventions for the two cylinder case, we find the following set of relations I α 1 m a 1 m a 2 I α 2 m a 3 α 1 r − a 1 a 3 = F r − T 1 r = F + T 1 = T 1 + T 2 = T 1 r − T 2 r = T 2 = α 2 r + a 2 = α 2 r − a 2 torque on first cylinder acceleration of the first cylinder acceleration of the second cylinder torque on second cylinder acceleration of the particle constraint on tangential acceleration at first cylinder constraint on tangential acceleration at second cylinder .
Solving these relations yields the tensions T 1 = 2 3 4 F and T 2 = 2 3 1 F , which give the acceleration of the particle a 3 = 2 3 1 m F .