Simple Question Complicated Answer - 2
A parabola lies completely in the first quadrant and is tangent to the line y = 3 x at ( 3 , 3 3 ) and to the x-axis at ( 4 , 0 ) . Find the distance between the vertex of the parabola and its focus (the focal distance).
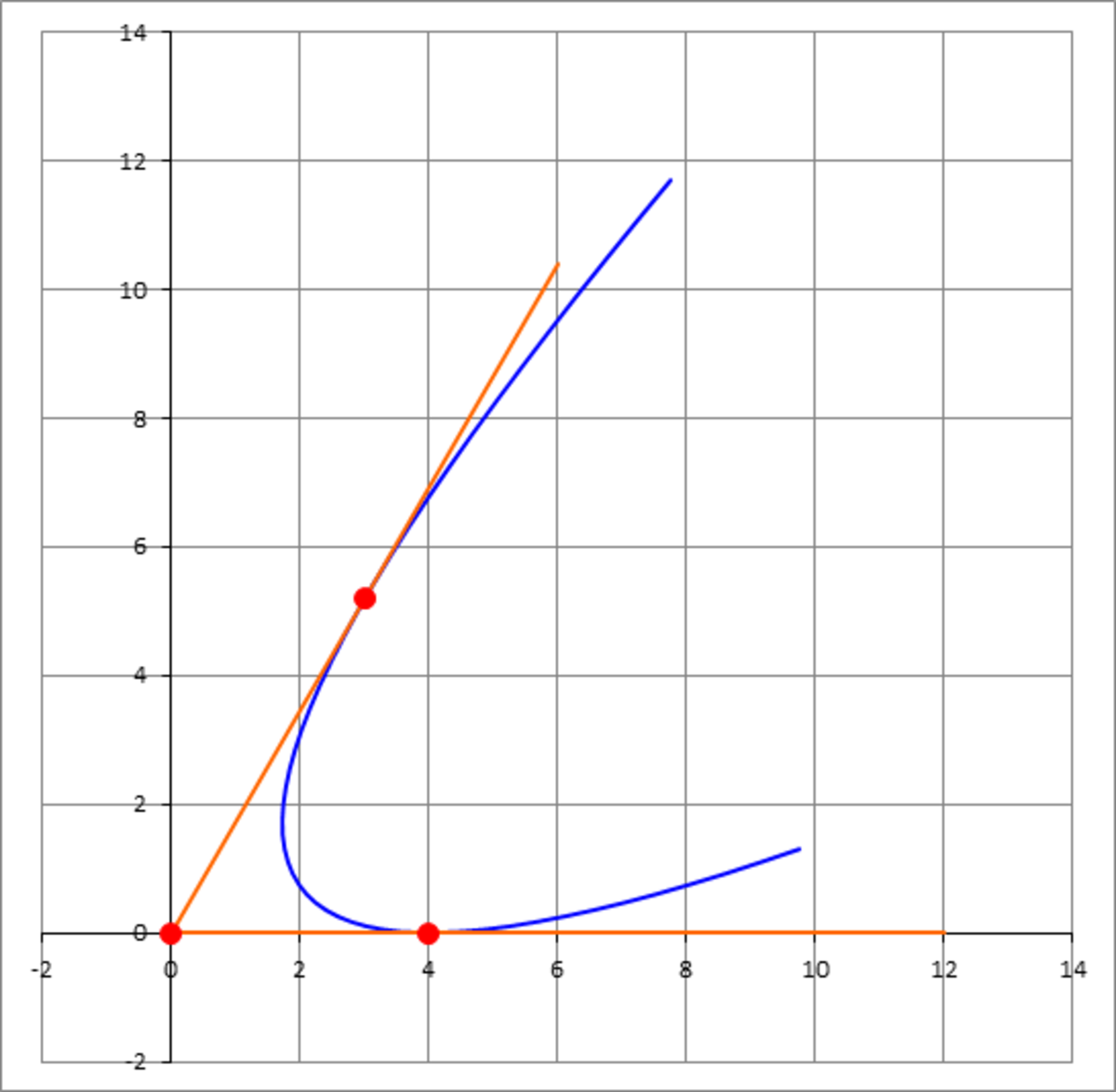
The answer is 0.652.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Very Elegant. Just wondering, how did you solve the three equations in the three unknowns. Did you do it yourself, or did you use Wolframalpha.com or a similar package ?
Log in to reply
For this one I used wolframalpha.com, but for other problems I sometimes use the rref matrix function on a graphing calculator (if the equations are linear) and sometimes I just solve them myself.
This problem lends itself to the Bezier curve method, which states the the parametric equation of the given parabola is,
p ( t ) = p 0 ( 1 − t ) 2 + 2 p 1 t ( 1 − t ) + p 2 t 2
where p 0 and p 2 are the tangent points of the parabola and p 1 is the intersection point of the two tangent lines.
So we can take p 0 = ( 4 , 0 ) , and p 2 = ( 3 , 3 3 ) and p 1 = ( 0 , 0 ) . Substituting this,
p ( t ) = ( 4 ( 1 − t ) 2 + 3 t 2 , 3 3 t 2 )
= ( 4 − 8 t + 7 t 2 , 3 3 t 2 )
= q 0 + q 1 t + q 2 t 2
where q 0 = ( 4 , 0 ) , q 1 = ( − 8 , 0 ) , q 2 = ( 7 , 3 3 )
Now we'll apply a small trick to orthogonalize the two axes spanning p ( t ) . Since the parameter t can be any real number, we can, just as well, use ( t − t 0 ) instead of t , where t 0 is some fixed real number. Thus
p ( t ) = q 0 + q 1 ( t − t 0 ) + q 2 ( t − t 0 ) 2
= ( q 0 − q 1 t 0 + q 2 t 0 2 ) + ( q 1 − 2 q 2 t 0 ) t + q 2 t 2
Now, we'll select t 0 such that,
( q 1 − 2 q 2 t 0 ) ⋅ q 2 = 0
which is always possible by choosing t 0 = 2 1 ( q 2 . q 2 ) ( q 1 . q 2 ) , then
p ( t ) = w 0 + w 1 t + w 2 t 2
where,
w 0 = q 0 − q 1 t 0 + q 2 t 0 2
w 1 = q 1 − 2 q 2 t 0
w 2 = q 2
and with the above value of t 0 , we have w 1 orthogonal to w 2 . If we now define unit vectors along w 1 and w 2 as follows
u 1 = w 1 / ∣ w 1 ∣ and u 2 = w 2 / ∣ w 2 ∣ , then
p ( t ) = w 0 + ∣ w 1 ∣ u 1 t + ∣ w 2 ∣ u 2 t 2
since u 1 and u 2 are unit vectors and are orthogonal, they specify a reference frame, hence
p ( t ) − w 0 = [ u 1 , u 2 ] ( x , y )
with x = ∣ w 1 ∣ t , and y = ∣ w 2 ∣ t 2
thus ( ∣ w 1 ∣ x ) 2 = ∣ w 2 ∣ y
is our equation of the parabola; it follows that y ( ∣ w 2 ∣ ∣ w 1 ∣ 2 ) = x 2
Comparing this with the standard equation of a parabola, which is 4 p y = x 2 , it follows that,
4 p = ∣ w 2 ∣ ∣ w 1 ∣ 2
which imples that p = 4 1 ∣ w 2 ∣ ∣ w 1 ∣ 2
The rest is straight forward computations.
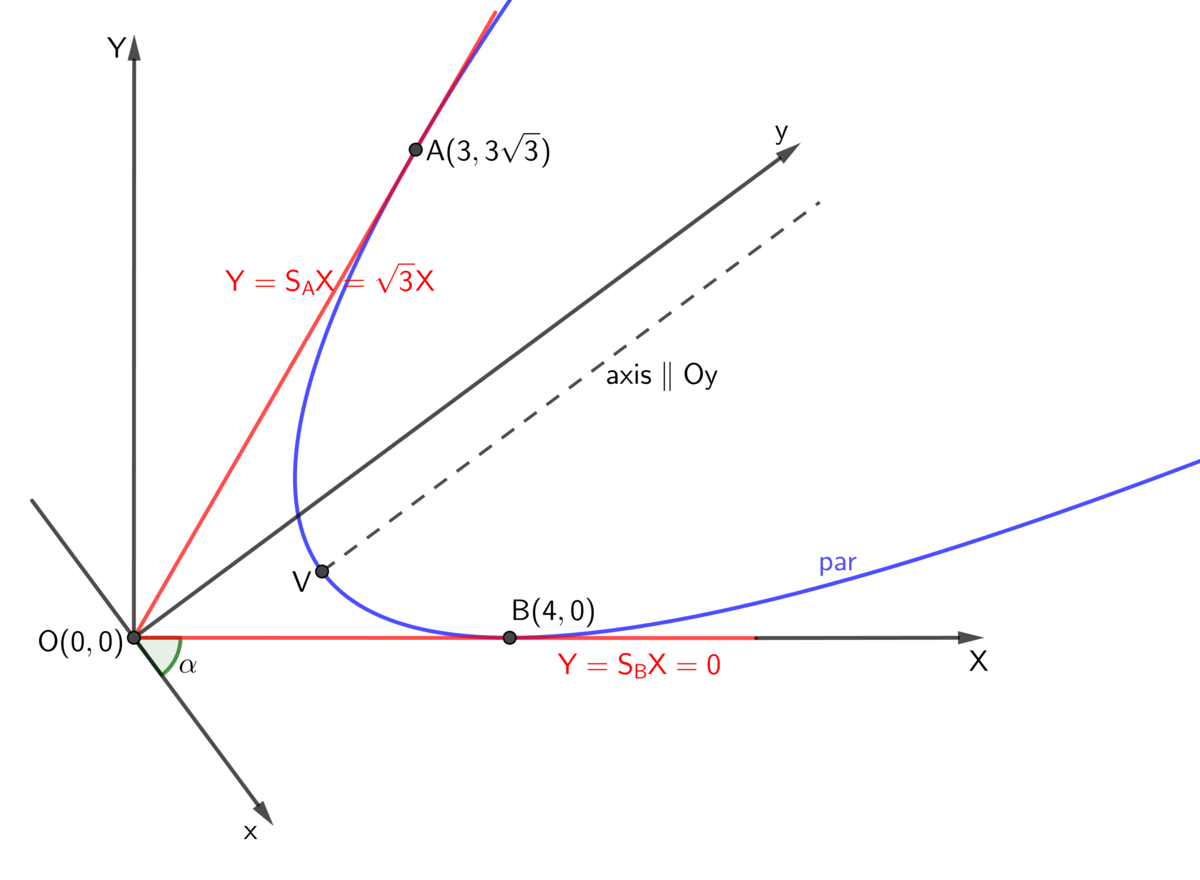
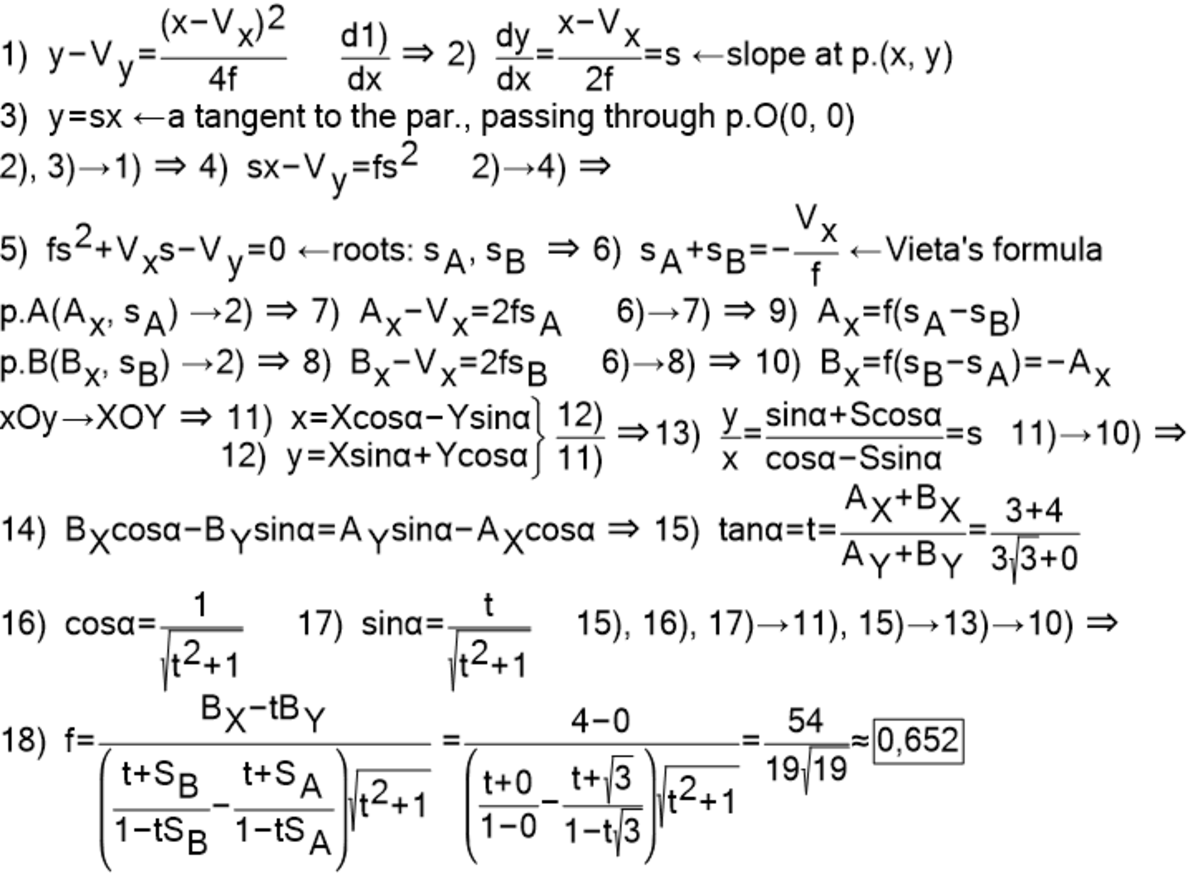
Label the three points A ( 0 , 0 ) , B ( 3 , 3 3 ) , and C ( 4 , 0 ) , and draw B C . By the distance formula, the sides of △ A B C are A C = 4 , A B = 6 , and B C = 2 7 . Now rotate and shift the diagram so that the parabola has a vertical axis and a vertex at ( 0 , 0 ) , for an equation of y = a x 2 , while still preserving the focal distance and triangle lengths of △ A ′ B ′ C ′ .
Let B ′ be ( u , a u 2 ) and C ′ be ( v , a v 2 ) . The slope at B ′ is y ′ = 2 a u so its tangent line is y = 2 a u x − a u 2 . Likewise, the tangent line at C ′ is is y = 2 a v x − a v 2 . These tangent lines intersect at A ′ ( 2 1 u + 2 1 v , a u v ) .
Using the distance formula for each side of △ A ′ B ′ C ′ gives
B ′ C ′ 2 = ( u − v ) 2 + ( a u 2 − a v 2 ) 2 = 2 8
A ′ C ′ 2 = ( 2 1 u − 2 1 v ) 2 + ( a u v − a v 2 ) 2 = 1 6
A ′ B ′ 2 = ( 2 1 u − 2 1 v ) 2 + ( a u v − a u 2 ) 2 = 3 6
which for a > 0 has a solution of a = 2 1 6 1 9 1 9 .
Therefore, the focal distance is p = 4 ⋅ 2 1 6 1 9 1 9 1 = 3 6 1 5 4 1 9 ≈ 0 . 6 5 2 .