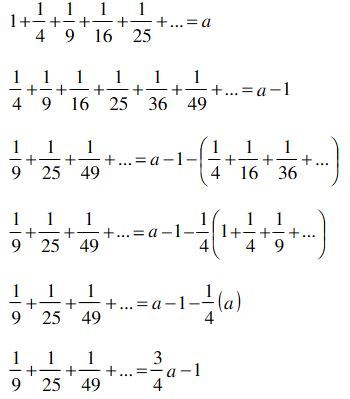Taking Every Other Term
a = 1 + 4 1 + 9 1 + 1 6 1 + 2 5 1 + ⋯
Determine the value of the below expression in terms of a .
9 1 + 2 5 1 + 4 9 1 + ⋯
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I too did it the same way as Muhammad Maulana but for the sake of variety here is a small trick.
Note that two options repeats twice so both of them are not the solutions since only one option is correct.
a ≈ 1 . 6 ( 6 π 2 ) .
3 a − 1 is negative ( ≈ − 0 . 4 6 ) but the required expression is a sum of positive terms leaving us with the only option 4 3 a − 1
Solution: