Simple Unit Squares and Lines
Three unit squares and two lines are shown. What is the area of triangle A B C ?
Express your answer as a decimal.
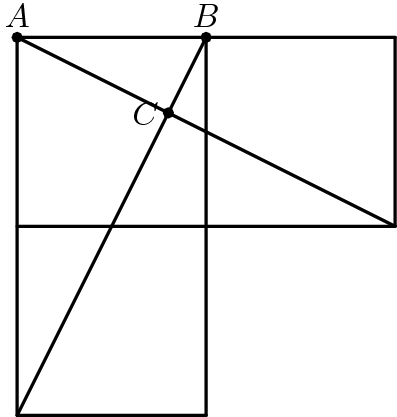
The answer is 0.2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
The triangle sought is a right triangle with hypotenuse A B = 1 . It is similar to the large right triangles formed, which have hypotenuse 1 2 + 2 2 = 5 and area 2 1 ∗ 1 ∗ 2 = 1 . The scale factor is thus 5 1 and so the area for the triangle is just the square of this. 5 1 = 0 . 2
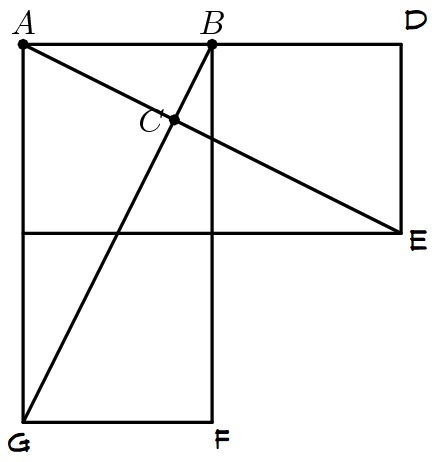 Since
△
B
F
G
≅
△
A
D
E
,
∠
A
C
B
=
9
0
. Since
△
A
C
B
∼
△
A
D
E
, we have
Since
△
B
F
G
≅
△
A
D
E
,
∠
A
C
B
=
9
0
. Since
△
A
C
B
∼
△
A
D
E
, we have
A C B C = A D D E
A C B C = 2 1
A C = 2 B C
By pythagorean theorem on △ A C B ,
1 2 = ( B C ) 2 + ( A C ) 2
1 = ( B C ) 2 + ( 2 B C ) 2
1 = 5 ( B C ) 2
B C = 5 1
It follows that, A C = 2 5 1 .
The area of △ A C B is
A = 2 1 ( C B ) ( A C ) = 2 1 ( 5 1 ) ( 2 5 1 ) = 5 1 = 0 . 2
Set up a coordinate system wih the origin at lower left.Call the point E.Let C be the intersection point,D lower right.E =(0,0), A= (0,3). B= (1,2), D = (2,1). Equation of line EB is y = 2x. Equation of line AD is y = (-1/2)x +2. The intersection point C = (.8,1.6). The product of slopes = -1, so the lines are perpendicular. CB = .447214, AC = .894417. Area of Area of ABC = (1/2) BC AC = .2 Ed Gray
Employ Cartersian coordinates - let the equations of the two diagonal lines be y = 2 x − 2 and y = − 2 x where the topmost and leftmost corner is taken to be the origin. Now x = − 2 y so we have:
y = 2 ( − 2 y ) − 2
y = − 4 y − 2
( 1 + 4 ) y = − 2
5 y = − 2
y = − 5 2
So the height of the triangle is 5 2 which means its area is 2 1 × 1 × 5 2 = 5 1 = 0 . 2 .
Let D be the point of intersection of the extension of A C with the vertical through B . Then Δ B C D and Δ A C B are similar, and since ∣ B D ∣ = 1 / 2 and ∣ A B ∣ = 1 the area of Δ A C B will be 4 tines that of Δ B C D . The area of Δ A B C will thus be 4 / 5 the area of Δ A B D , which is 1 / 4 , giving us an answer of 4 / 5 × 1 / 4 = 1 / 5 = 0 . 2 .