Simple yet complex

Classical Mechanics Level 5

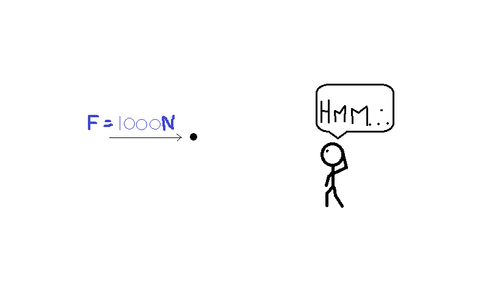A particle of mass 1Kg is kept at rest at the origin. A constant force 1000N starts acting on it at t=0. Find the speed of particle at time t=10^6 sec . Let the answer be (a x 10^8) Find a.(Rounding off to 1 decimal place)


The answer is 2.9.

Ritesh Yadav by Ritesh Yadav , 24, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Mvs Saketh
Aug 10, 2014

It's a relativistic problem, though the actual solution involves deriving the expression for speed of light for a relativistic particle using the fact that mass changes as

m = m ( r e s t ) 1 − v 2 c 2 m=\frac { m(rest) }{ \sqrt { 1-\frac { { v }^{ 2 } }{ c^ 2 } } }

However a cheap trick is that, since the velocity as per classical mechanics is 10^9 at the time, which is impossible as it exceeds speed of light, so the no, just smaller than speed of light by one decimal point is 2.9 * 10^8 m/s

6 Helpful 0 Interesting 0 Brilliant 0 Confused

you have to mention that we have to use modern physics.

safa m - 6 years, 5 months ago

m = m ( r e s t ) 1 − v 2 c 2 m=\frac { m(rest) }{ \sqrt { 1-\frac { { v }^{ 2 } }{ c^ 2 } } }

Mardokay Mosazghi - 6 years, 10 months ago

well this isn't fair!!! 2.99 is as acceptable as 2.9!! so why doesnt it take it!!??

A Former Brilliant Member - 6 years, 7 months ago

Log in to reply

The question states "rounding off to 1 decimal place".

Calvin Lin Staff - 6 years, 7 months ago

This is not classical Mechanics, though including it here makes it more tricky as we expect a different outcome xD

Pratyush Pandey - 4 years, 7 months ago

Simple yet complex

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...