Simplify first!
Solve the following equation for x ∈ [ 0 , 2 π ]
sin ( 3 x ) sin 3 ( x ) + cos ( 3 x ) cos 3 ( x ) = sin 6 ( 2 x )
You may use the fact that u 4 − u 3 − u 2 + u + 1 = 0 has no real solution.
Submit your answer in radian!
The answer is 0.452278447.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I think there is better solution than mine.
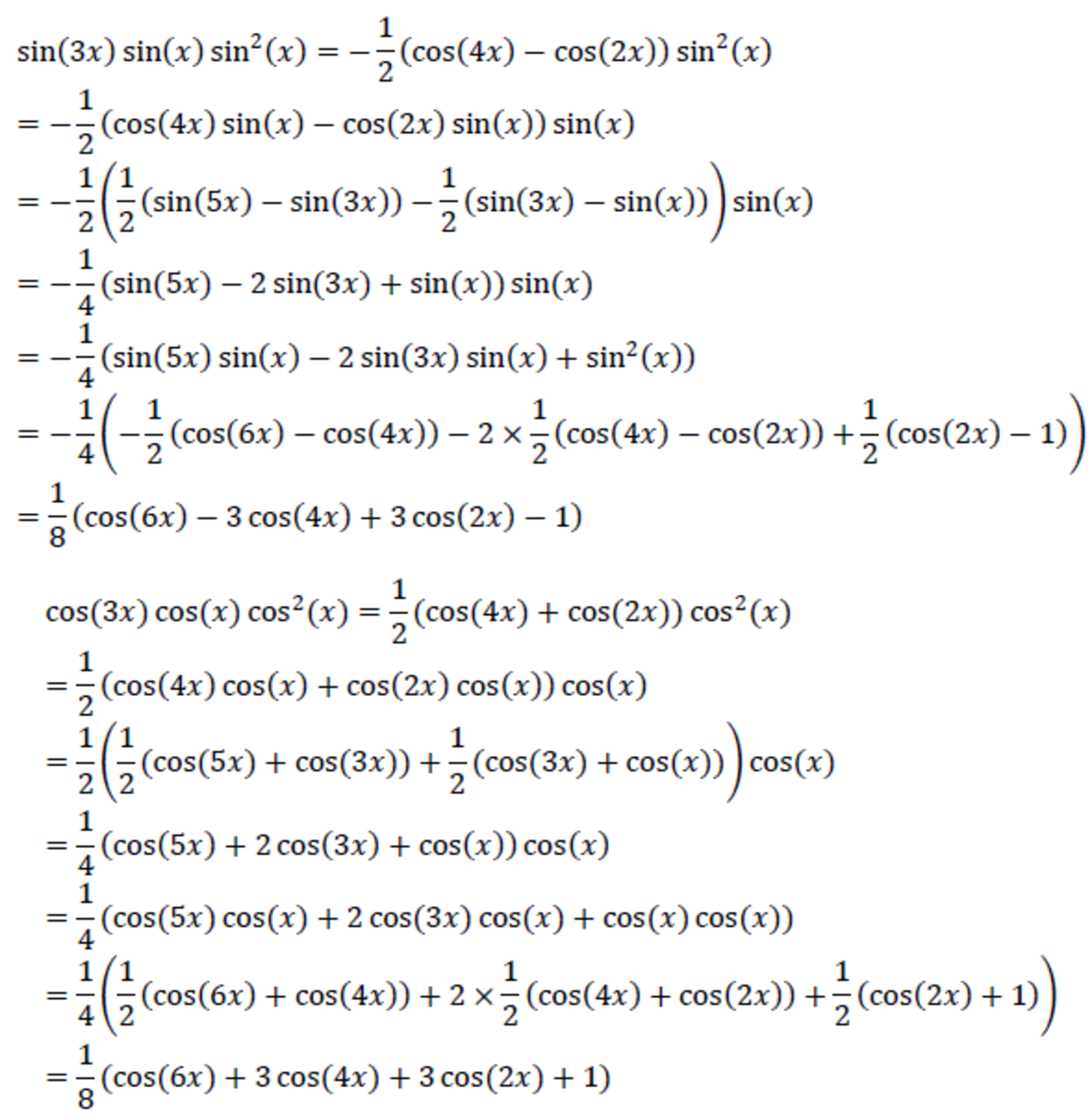
Combine the two equations and using the fact that cos ( 3 x ) = 6 cos 3 ( u ) − 3 cos ( u ) , we get
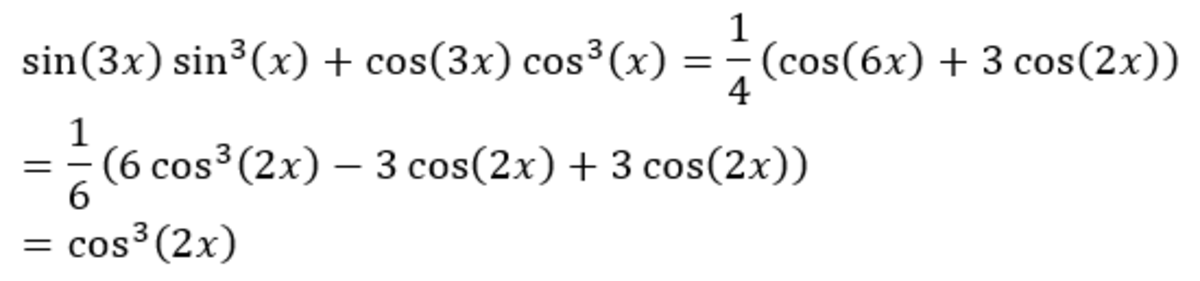
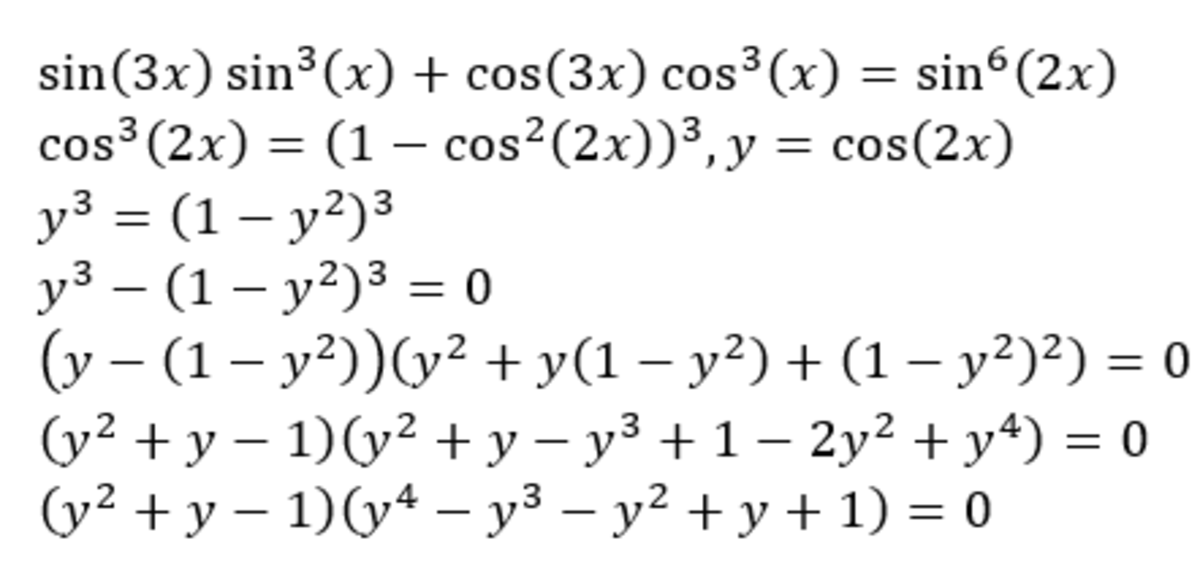
The second factor have no real solution. Using quadratic formula and because ∣ y ∣ ≤ 1 , we get the solution from the first factor
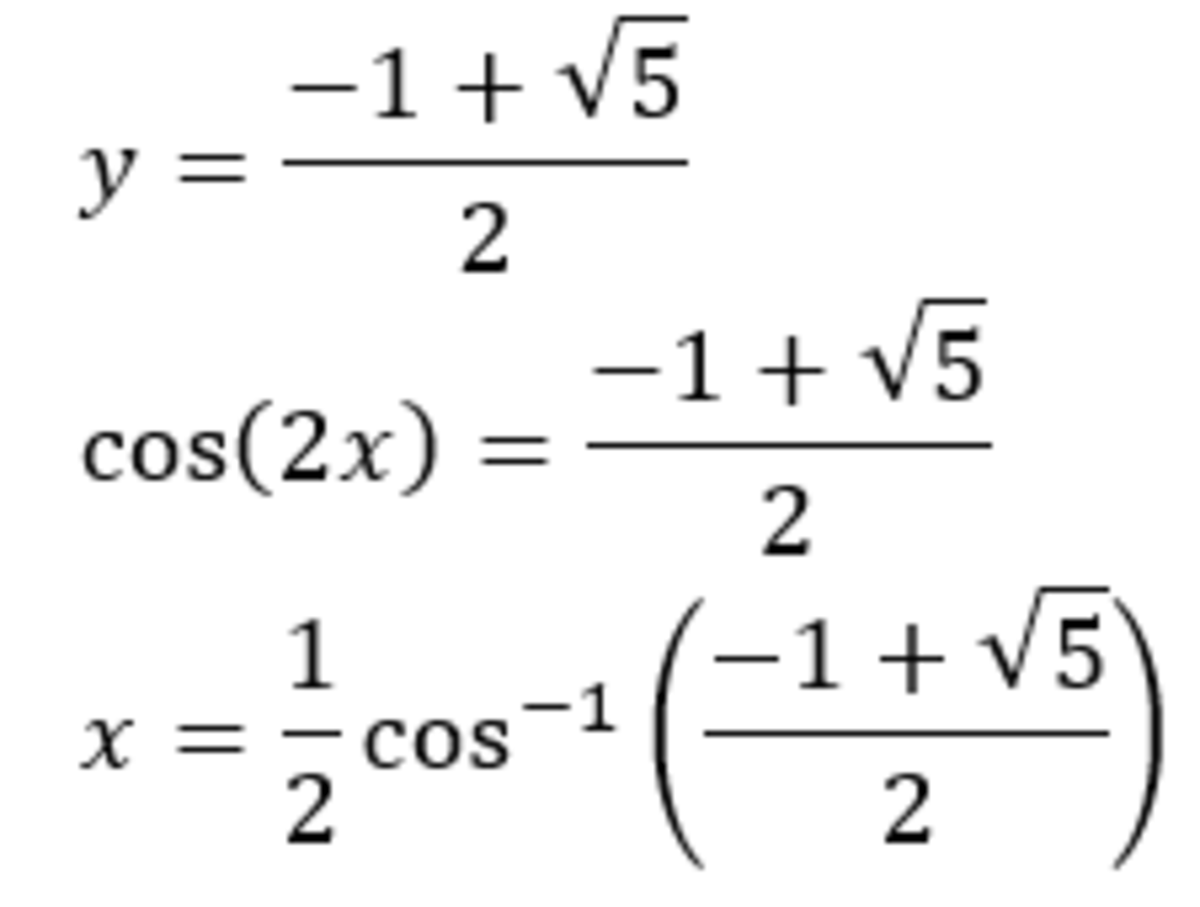
I calculated the angle in degrees unit :)
sin ( 3 x ) sin 3 x + cos ( 3 x ) cos 3 x 2 cos ( 2 x ) − cos ( 4 x ) ⋅ 2 1 − cos ( 2 x ) + 2 cos ( 2 x ) + cos ( 4 x ) ⋅ 2 1 + cos ( 2 x ) 2 cos ( 2 x ) + cos ( 2 x ) cos ( 4 x ) cos ( 2 x ) + 2 cos 3 ( 2 x ) − cos ( 2 x ) cos 3 ( 2 x ) cos 3 ( 2 x ) cos ( 2 x ) cos 2 ( 2 x ) + cos ( 2 x ) − 1 cos ( 2 x ) 2 x ⟹ x = sin 6 ( 2 x ) = sin 6 ( 2 x ) = sin 6 ( 2 x ) = 2 sin 6 ( 2 x ) = sin 6 ( 2 x ) = ( 1 − cos 2 ( 2 x ) ) 3 = 1 − cos 2 ( 2 x ) = 0 = 2 5 − 1 ≈ 0 . 9 0 4 5 5 6 8 9 4 ≈ 0 . 4 5 2