Simultaneous Radical Equations!
x + y y + x = 1 1 = 7
Let n be the number of real pairs ( x , y ) to the above system of equations. Define these solution pairs as ( x 1 , y 1 ) , … , ( x n , y n ) . Let
S = i = 1 ∑ n ( x i + y i ) .
Find n + S .
The answer is 14.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
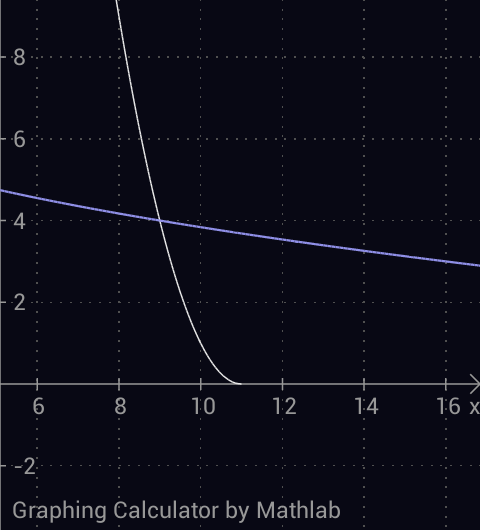 Sketch or graph the two equations. You'll see they intersect only at one point. Some exploration will show that the point is (9, 4). Hence the answer is 1+9+4=14.
[P.S. Also note that
x
≤
1
1
and
y
≤
7
which greatly decreases the checking work you have to do.]
Sketch or graph the two equations. You'll see they intersect only at one point. Some exploration will show that the point is (9, 4). Hence the answer is 1+9+4=14.
[P.S. Also note that
x
≤
1
1
and
y
≤
7
which greatly decreases the checking work you have to do.]
Put x=sec^2z and y=tan^2z and solve the equations. You will get only one solution satisfying the given equations i.e. x=9 and y=4. Hence the answer is 1+9+4 = 14
I don't understand how the substitution is justified. In effect you're assuming that x=y+1. Could you please explain?