sin ( cos x ) vs. cos ( sin x )
If 0 < x < 2 π , then which is greater?
A = sin ( cos x )
B = cos ( sin x )
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
B = cos ( sin x ) = sin ( 2 π − sin x ) . Since sin x + cos x = 2 sin ( x + 4 π ) ≤ 2 < 2 π . Then 2 π − sin x > cos x . Therefore, B = sin ( 2 π − sin x ) > sin ( cos x ) = A or B > A .
Sir,please check my solution
Log in to reply
I'm not sure. At first I was also trying this approach.
Ok sir,thanks for paying attention
In the folllowing range we can,say that sinx<x......(1) ..so,cos(sinx)>cosx.....(2) Put...x=cosx in equation 1.. So,cosx>sin(cosx)......(3) Therefore, Cos(sinx)>sin(cosx)......... Please comment if you figure out some mistake
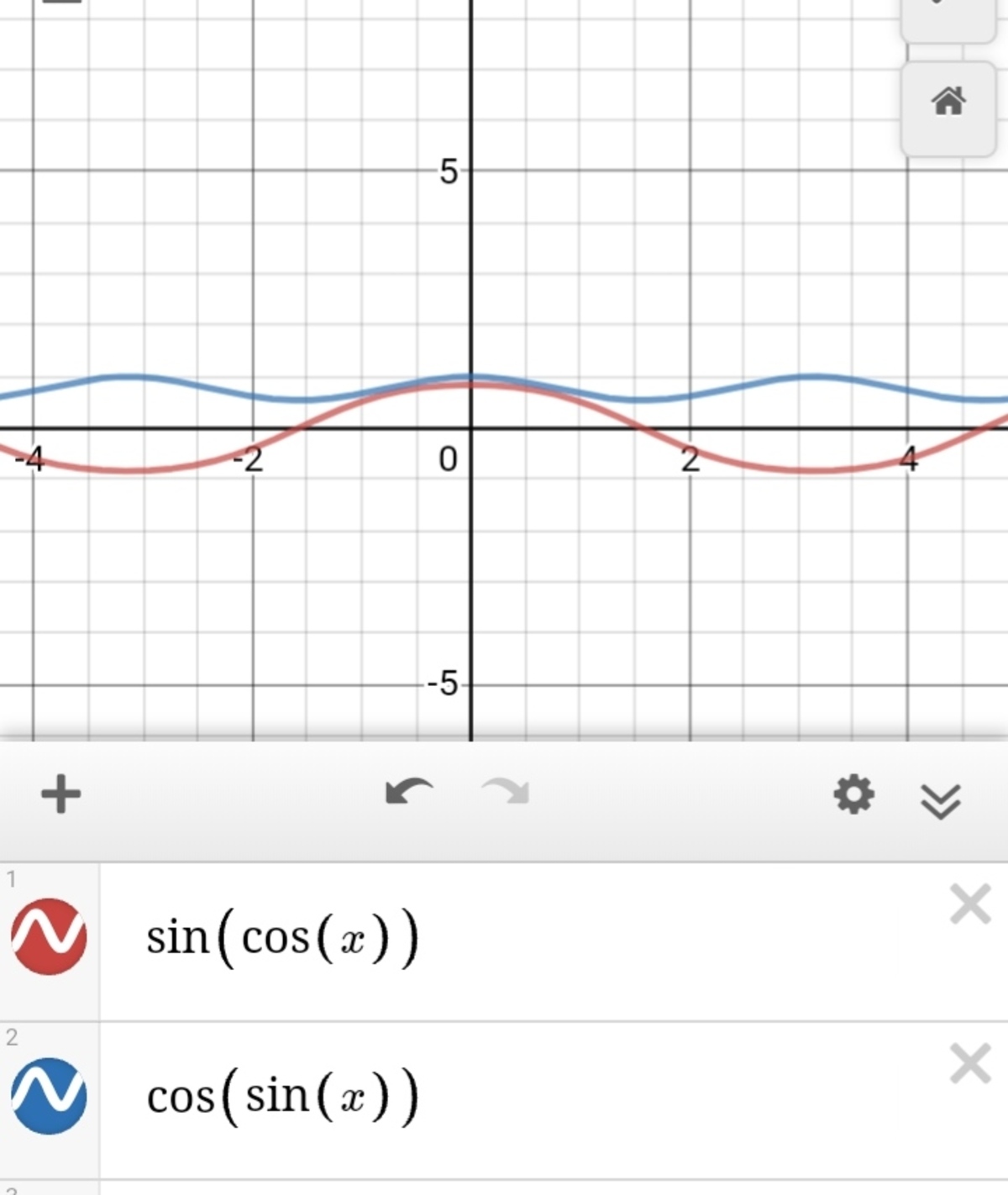
sin x + cos x ≤ 2 < 2 π (since 3 < π < 4 and 8 < 9 ⟹ 2 < 1 . 5 ), therefore cos x < 2 π − sin x ⟹ sin ( cos x ) < sin ( 2 π − sin x ) = cos ( sin x )