0.96
If 0 < θ < 2 π and sin θ = 2 5 2 4 , what is the value of
sin 2 θ + cos 2 θ cos 2 θ ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
sin(theta)=24/25 so (theta)=sin inverse of 24/25 which is 73.74 nw substitute in place of theta as 73.74
Let x= cos (theta), y= sin(theta). Let alpha= cos(theta/2), beta=sin(theta/2).
Let the value of the given expression be V. Then.
V=alpha/(alpha+beta)
=alpha(alpha-beta)/(alpha^2-beta^2)
= (2alpha^2-2alpha beta)/[2(alpha^2-beta^2)]
From the definitions of alpha and beta,
2 alpha beta= sin(theta)=y
2 alpha^2-1=alpha^2-beta^2=cos(theta)=x, i.e., 2 alpha^2=1+x
Therefore,
V=(1+x-y)/(2x)
y=24/25 implies x= 7/25 (since x^2+y^2=1)
Therefore, V= (25+7-24)/14=8/14=4/7
It is easier if you multiply it by 2\sin(\frac{theta}{2}). Farzad Saeidi - now

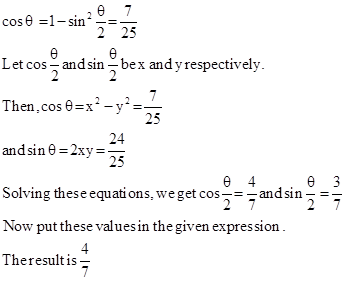
It is given that: sin θ = 2 5 2 4
⇒ cos θ = 1 − ( 2 5 2 4 ) 2 = 2 5 2 2 5 2 − 2 4 2 = 2 5 2 ( 2 5 − 2 4 ) ( 2 5 + 2 4 ) = 2 5 2 4 9 = 2 5 7
sin 2 θ + cos 2 θ cos 2 θ = sin 2 θ + cos 2 θ cos 2 θ × 2 cos 2 θ 2 cos 2 θ = 2 sin 2 θ cos 2 θ + 2 cos 2 2 θ 2 cos 2 2 θ = 2 sin 2 θ cos 2 θ + 2 cos 2 2 θ − 1 + 1 2 cos 2 2 θ − 1 + 1 = sin θ + cos θ + 1 cos θ + 1 = 2 5 2 4 + 2 5 7 + 1 2 5 7 = 5 6 3 2 = 7 4