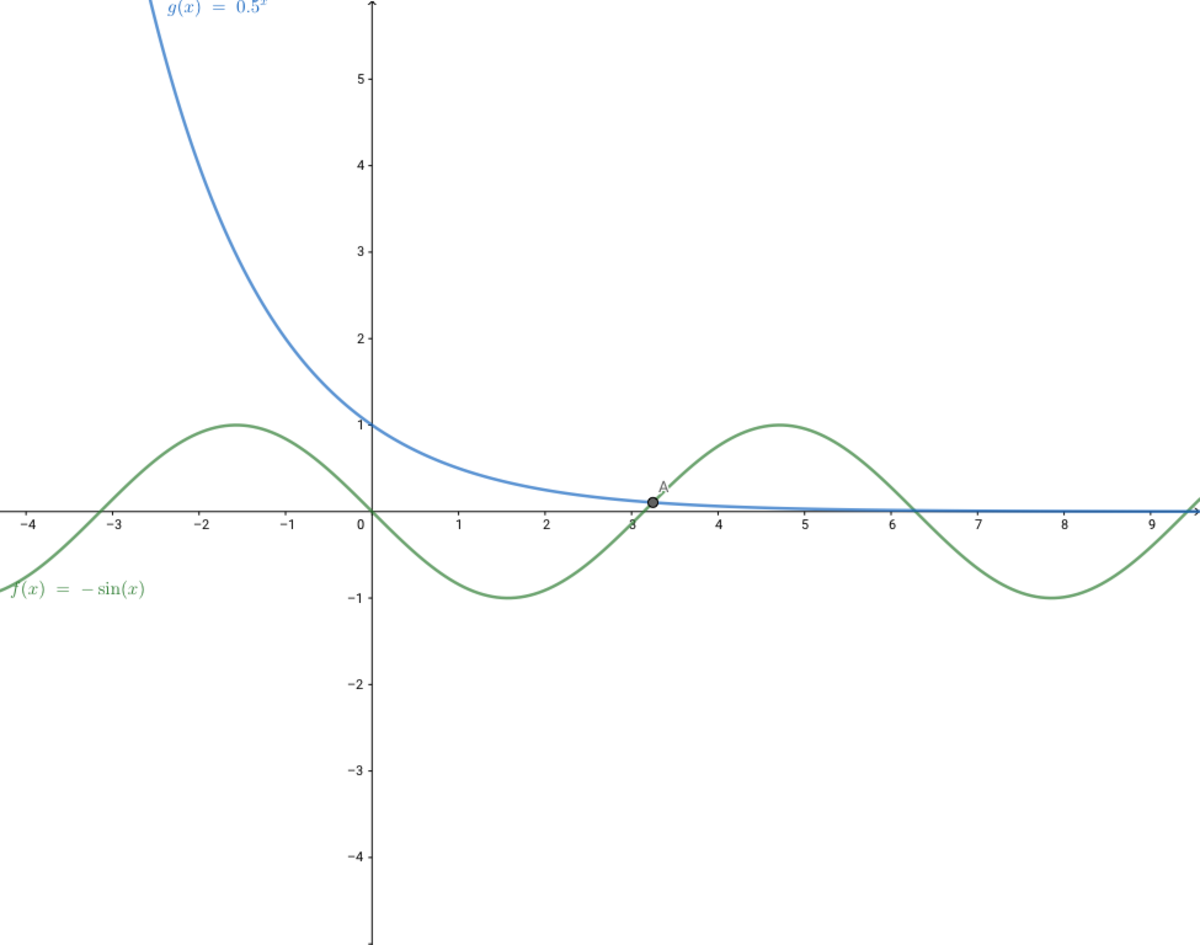
The equation between $-\sin x$ and $\left(\frac 12\right)^x$

The function $y=-\sin x$ in $\left(0,\dfrac{\pi}{2}\right), \left(\dfrac{3\pi}{2},2\pi\right)$ is the minus function, in $\left(\dfrac{\pi}{2}, \dfrac{3\pi}{2}\right)$ is the increase function. $-\sin 0=-\sin 2\pi =0, -\sin \dfrac{\pi}{2}=-1, -\sin \dfrac{3\pi}{2}=1$ The function $y=-\sin x$ at $x=\dfrac{3\pi}{2}$ . There is a maximum of $1$ , $y=-\sin x$ at $x=\pi$ . It has a minimum of $-1$ . Because the function $y=\left(\dfrac{1}{2}\right)^x$ , Within the interval $(0,100\pi)$ is the minus function. $x>0,y\in(0,1)$ Therefore, the above equation has two solutions in interval $(0,2\pi)$ . In $x\in (0,100\pi)$ , The function $y=-\sin x$ , There are $50$ cycles. So there are $100$ solutions to this equation. The answer is $100$ .

Consider the function $f(x) = (1/2)^x + \sin x$ on $[(2k+1)\pi \;,\; (4k+3)\pi/2]$ for $k = 0, 1, \cdots, 49$ , and note that:

• $f$ is continuous on $[(2k+1)\pi \;,\; (4k+3)\pi/2]$ ,
• $f((2k+1)\pi) = (1/2)^{(2k+1)\pi} + \sin((2k+1)\pi) = (1/2)^{(2k+1)\pi} > 0$ , and
• $f(4k+3)\pi/2) = (1/2)^{(4k+3)\pi/2} + \sin((4k+3)\pi/2) = (1/2)^{(4k+3)\pi/2} - 1 < 0$

By the Intermediate Value Theorem, there is a number $\alpha_k \in ((2k+1)\pi \;,\; (4k+3)\pi/2)$ such that $f(\alpha_k) = 0$ .

We now show that $\alpha_k$ is the only root of $f$ on the prescribed domain. Indeed, if $\gamma_k$ is another root, then:

• $f$ is continuous on $[(2k+1)\pi \;,\; (4k+3)\pi/2]$ ,
• $f$ is differentiable on $((2k+1)\pi \;,\; (4k+3)\pi/2)$ , and
• $f(\alpha_k) = f(\gamma_k) = 0$

By Rolle’s Theorem, there is a number $\delta \in ((2k+1)\pi \;,\; (4k+3)\pi/2)$ such that $f’(\delta) = 0$ . However, $f’(\delta) = (1/2)^{\delta} \ln(1/2)+ \cos \delta < 0$ yielding a contradiction.

Now consider $f(x) = (1/2)^x + \sin x$ on $[(4k+3)\pi/2 \;,\; (2k+2)\pi]$ for $k = 0, 1, \cdots, 49$ . A similar argument as before shows that there is a unique number $\beta_k \in ((4k+3)\pi/2 \;,\; (2k+2)\pi)$ such that $f(\beta_k) = 0$ .

Since $f$ has exactly $100$ roots on $(0,100\pi)$ , $-\sin x = (1/2)^x$ has $100$ solutions on $(0,100\pi)$ .