Cos(Sin) = Sin(Cos)?
cos ( p ⋅ sin x ) = sin ( p ⋅ cos x ) Find the smallest positive integer p for which the above equation has a solution for x ∈ [ 0 , 2 π ] .
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
The easiest way to show this is to plot f ( x ) = cos ( p sin x ) − sin ( p cos x ) for various values of p . I have done that for p = 1 , 2 , 3 with a spreadsheet. And the graph is as follows:
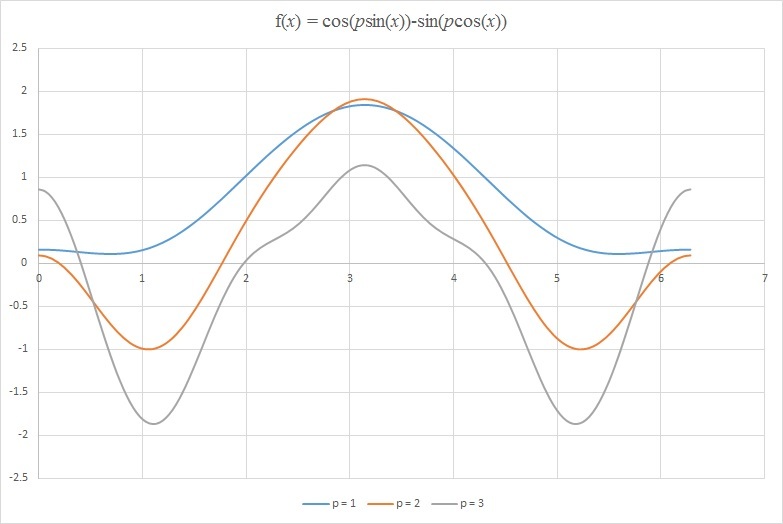
It is note that p = 1 (blue line) has no solution. When p = 2 (red line) and p = 3 (green line) each has 4 solutions. Therefore, the smallest p with solutions is 2 .
The label for the graph does not agree with the text of the solution. Which formula was actually used to make the plot?
Log in to reply
Sorry, I had plotted the wrong graph. I have done a new one. Thanks for your inquiry.
Simplifying the equation with
Vishnu C's Method
would give you the final equation as
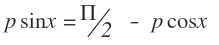 which further reduces to
which further reduces to
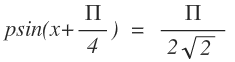 . Now since
RHS is greater than 1
therefore for x to exist p must be greater than 1. So lowest possible Integer will be
p=2
.
. Now since
RHS is greater than 1
therefore for x to exist p must be greater than 1. So lowest possible Integer will be
p=2
.
As the result of a cos and sin can only be the same if
cos(x)=sin(PI/2 - x)
Then here we have:
p cos (x) = PI/2 - p sin(x) , or
PI/2 = p ( cos(x) + sin(x) )
As the maximum of cos(x)+sin(x) is sqrt(2), then to reach PI/2 in above, integer p has to be:
p >= sqrt(2) PI /2 = 1.11 => p = 2 or higher
Here, I've used only two trigonometric identities: s i n ( x + 2 π ) = c o s ( x ) a n d s i n ( 2 π − x ) = c o s ( x ) . First, simplify the result that you get using the latter identity. Now, if you check the case for which p s i n x + p c o s x = π / 2 ⇒ p s i n ( x + 4 π ) = 2 2 π , you can clearly see that it's not possible for p>=1 as it would take a negative x to satisfy the equation. So, we try the next thing, which is p s i n ( 4 π − x ) = 2 2 π ; and we can see that even for this equation, p=1 is not going to work. Now, if we try p=2, take the sine inverse and subtract the result from π / 4 , we can see that the x thus obtained is between 0 and 2 π . In addition to this, we can also see that 2 2 π > 1 and therefore, a value of p=1 will never satisfy the set of solutions to the equation for any real x. As 1 is removed and 2 confirmed, the answer is 2.