sinA/a
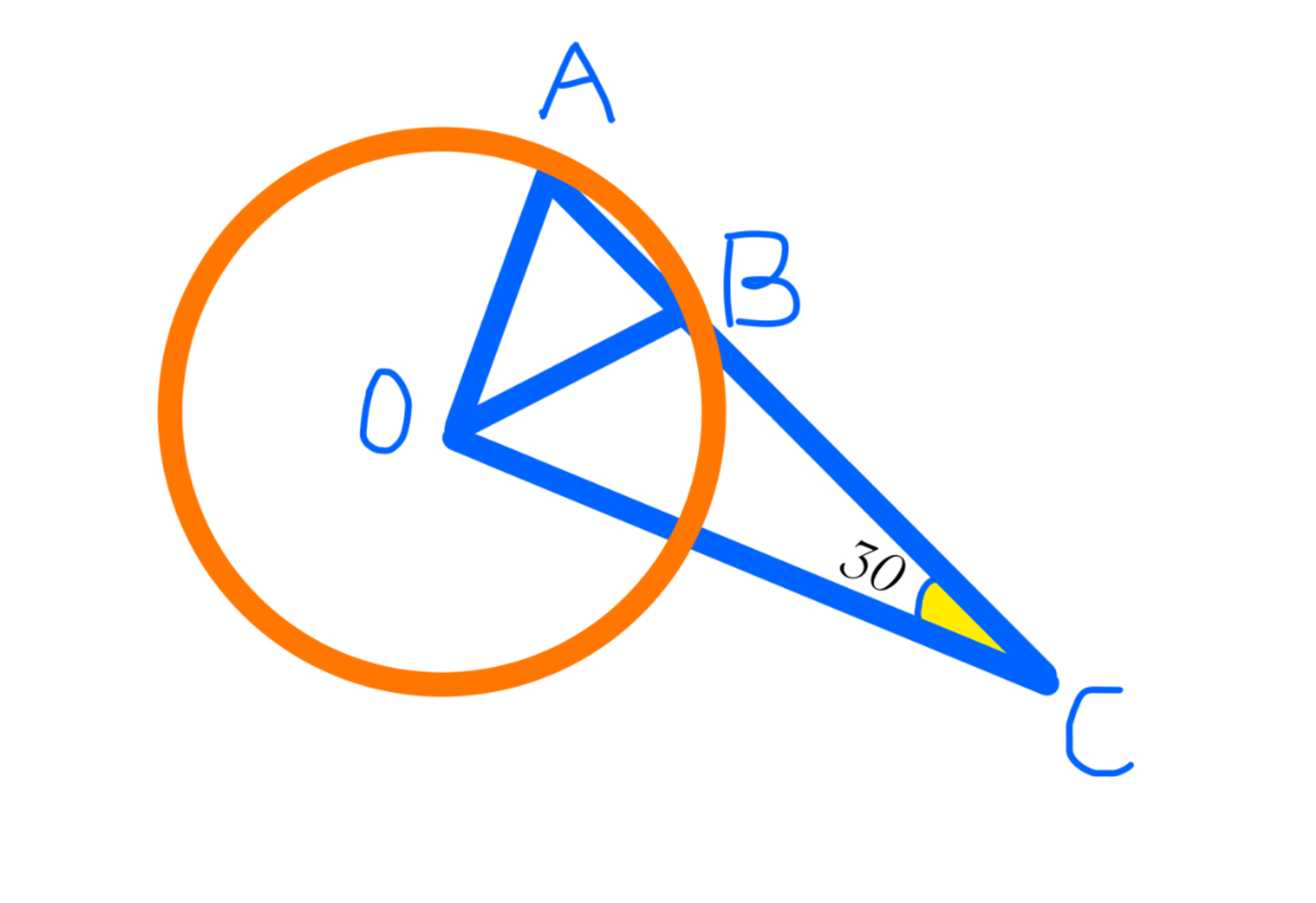
Given that point O is the center of the circle and O A = 5 , O C = 8 , and ∠ A C O = 3 0 ∘ , find ∠ B O A in degrees. Type 0 if you think this problem is unsolvable.
The answer is 73.7398.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
This one pretty much qualifies as being unsolvable in ""degrees"".
Draw the median O M of △ A O B where M is the midpoint of A B .
Since △ A O B is isosceles, ∠ O M B is a right angle, and solving right triangle △ O M C with O C = 8 and ∠ A C O = 3 0 ° gives O M = 4 , and solving right triangle △ M O A with O M = 4 and O A = 5 gives ∠ M O A = cos − 1 5 4 .
Therefore, ∠ A O B = 2 ∠ M O A = 2 cos − 1 5 4 ≈ 7 3 . 7 3 9 8 ° .
@David Vreken I just noticed that 2 cos − 1 n + 2 sin − 1 n = 1 8 0 ∘ 🧐
We can apply the cosine law on both the triangles COB and COA to find the missing side then subtract AC-CB to get AB and then use that to find the angle as we have the 3 sides in the triangle ABO with the cos law
∠ O A B ∘ = ∠ O B A ∘
In △ A O C : sin ( 3 0 ∘ ) 5 = sin ( ∠ O A C ∘ ) 8 ⟹ ∠ O A C ∘ ≈ 5 3 . 1
∠ B O A ∘ ∠ B O A ∘ ∠ B O A ∘ = 1 8 0 ∘ − ∠ O A B ∘ − ∠ O A B ∘ = 1 8 0 ∘ − 2 ( 5 3 . 1 ∘ ) = 7 3 . 7 3 ∘
Using sine law on triangle OBC,we get s i n ( A B O ) = 5 4
And the answer follows immediately using the fact that the sum of the angles of a triangle sum up to 180 degree and OA=OB
Using the sine rule,
O
A
s
i
n
∠
A
C
O
=
O
C
s
i
n
∠
O
A
C
.
So,
5
0
.
5
=
8
s
i
n
∠
O
A
C
, i.e.
s
i
n
∠
O
A
C
=0.8.
Therefore,
∠
O
A
C
=
s
i
n
−
1
0
.
8
=
5
3
.
1
3
0
1
0
.
.
.
Since the interior angles of a triangle add up to
1
8
0
∘
and OA & OB are the radii of the same circle i.e. triangle OAB is isosceles,
∠
A
O
B
=
1
8
0
∘
−
2
×
∠
O
A
C
=
7
3
.
7
3
9
7
9
5
.
.
.
So the answer is 73.739795...
Hey Jeff, great problem! However, angles are usually denoted counter-clockwise. The angle AOB would therefore refer to angle of size 360° - 73.739...° = 286.26...°.
I would suggest to change the angle we are looking for to BOA to make the problem clearer and mathematically correct.
Log in to reply
OK, I have fixed it :)
I guess it is understood that AOB refers to the acute angle here
Nice question. Was this the question you were trying to ask in discussion?
Log in to reply
No :) I didn’t ask the question, but yes, I was inspired by the discussion.
sin 3 0 ° 5 = sin ∠ O B C 8 = sin ∠ O B A 8
⟹ ∠ O B A = sin − 1 ( 5 4 ) ≈ 5 3 . 1 3 0 1 °
⟹ ∠ A O B = 1 8 0 ° − 2 × ∠ O B A ≈ 7 3 . 7 3 9 8 ° .