Sine and Cosine mixture
Find the minimum value of the given expression
( 2 cos α + 5 sin β − 8 ) 2 + ( 2 sin α + 5 cos β − 1 5 ) 2
The answer is 100.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
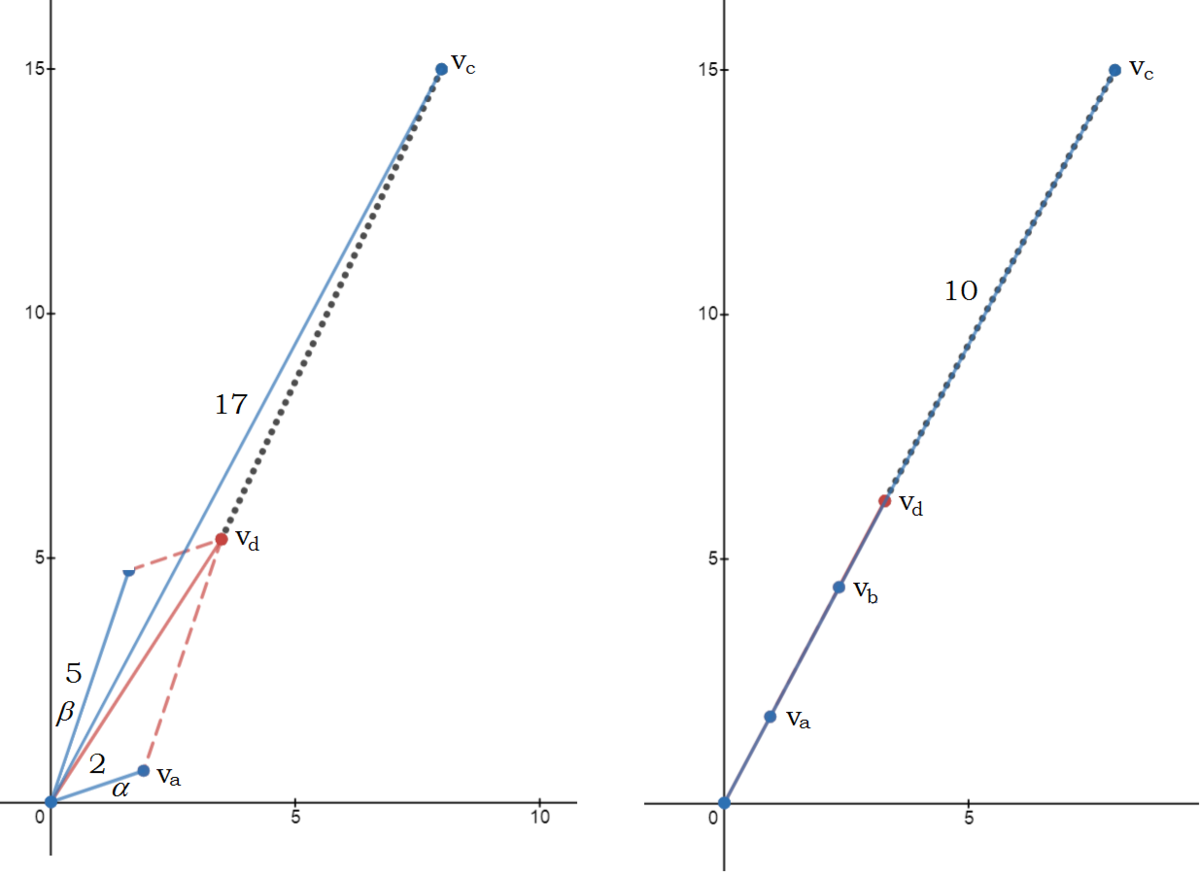
Consider three vectors v a = ( 2 cos α , 2 sin α ) , v b = ( 5 sin β , 5 cos β ) , and v c = ( 8 , 1 5 ) . Let v d = v a + v b . Then ( 2 cos α + 5 sin β − 8 ) 2 + ( 2 sin α + 5 cos β − 1 5 ) 2 = ∣ v d − v c ∣ 2 . And ∣ v d − v c ∣ (denoted by the dotted line) is minimum when α = tan − 1 1 5 8 and β = tan − 1 8 1 5 . Then we have
∣ v d − v c ∣ = ∣ v c − v d ∣ = ∣ v c ∣ − ∣ v d ∣ = 8 2 + 1 5 2 − ∣ v a ∣ − ∣ v b ∣ = 1 7 − 2 − 5 = 1 0
Therefore ∣ v c − v d ∣ 2 = 1 0 2 = 1 0 0 .

Consider the three vectors v 1 = ( 2 cos α , 2 sin α ) , v 2 = ( 5 sin β , 5 cos β ) , v 3 = ( − 8 , − 1 5 ) , then
the indicated sum is the square of the magnitude of v 1 + v 2 + v 3 , we can choose α and β so that v 1 and v 2 point in the opposite direction as v 3 , hence the length of the resultant vector is ( − 8 ) 2 + ( − 1 5 ) 2 − 2 − 5 = 1 7 − 7 = 1 0 , so that the square of the magnitude is 1 0 2 = 1 0 0 .