Sine Logarithm

Easy way is to draw the graphs of each $y=\log_{10}{x}$ and $y=\sin{x}$ Second one's maximum is 1 and First one is an increasing function. So we'll get 3 points of intersectio n

Solution 1: From the problem, we have 2 functions, $f(x)=\log_{10}{x}$ and $g(x)=\sin(x)$ . Notice, the function $g(x)$ never reaches above 1, and we cannot take the logarithm of a negative number. So, the lower bound of the domain is 0, and the upper bound of the domain is the point where $\log_{10}{x}=1$ . We can now solve for the upper bound: $\log_{10}{x}=1 \\ x = 10^1= 10$ Examining this domain, we notice that $g(x)$ cycles through just over $\frac{3}{2}$ periods, since each period is of length $2\pi \approx 6.28$ . Now, notice $f(x)$ only reaches a positive value when $x>1$ and continues to steadily increase. Also, notice that $g(x)$ first reaches 1 at x coordinate $\frac{\pi}{2}$ , and slowly goes back down towards 0. Therefore, during this interval, $f(x)$ must equal $g(x)$ at 1 point. When we get to $x=2\pi$ , the function $g(x)$ becomes positive again, reaches back to 1 and goes back down to zero at $x=3\pi$ . Therefore, during this interval, $f(x)$ must equal $g(x)$ twice. Adding up our results, we get $1+2=\boxed{3}$ .

Solution 2: We can simplify the equation given to us: $\log_{10}{x}=\sin(x)\\ x=10^{\sin(x)}, x>0$ From this new equation, we are able to obtain the functions $f(x)=x$ and $g(x)=10^{\sin(x)}$ . Notice, $g(x)$ never reaches above 10. Therefore, we only need to focus on the domain $(0,10]$ . Because the only place x appears in $g(x)$ is in the sine function, the function is periodic. Notice, $g(0)=1$ and $g'(0)=\ln(10)>1$ , therefore, $g(x)$ starts above $f(x)$ in the given interval and increases faster than $f(x)$ . Once $g(x)$ gets to $\frac{\pi}{2}$ , it reaches its peak at 10 and comes back downward to $\frac{1}{10}$ at $x=\frac{3\pi}{2}$ . Therefore, during that interval, $f(x)$ intersects $g(x)$ once. After x becomes greater than $2\pi$ , $g(x)$ increases back up to 10 and comes back downward to $10^{\sin(10)}$ at $x=10$ . Notice, $\sin(10)<0$ , therefore, the value of $g(x)$ becomes fractional by the end of the interval $(0,10]$ . Therefore, during the last interval $[2\pi,10]$ , $g(x)$ intersects $f(x)$ twice. Adding up our results, we get $1+2=\boxed{3}$

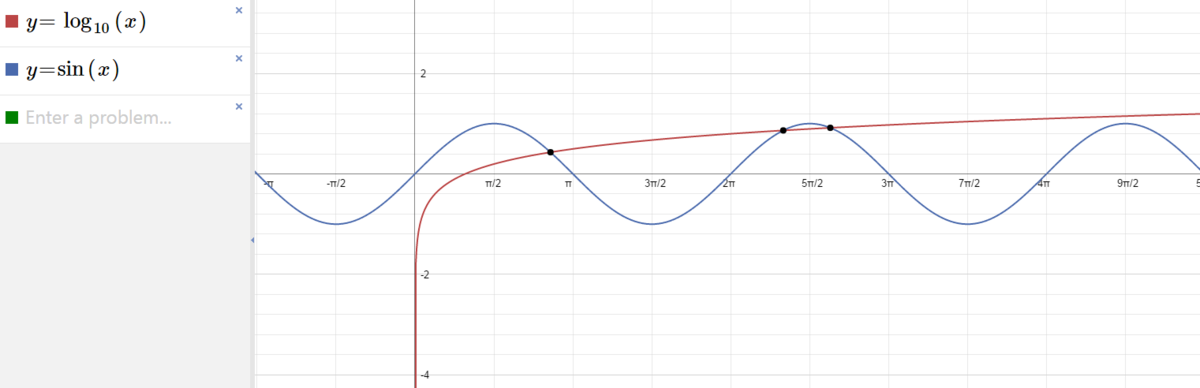Plot the graphs of the two functions given. Then you will find that the two functions will have 3 intersections. These 3 intersections are the solutions of the given question.