Sine
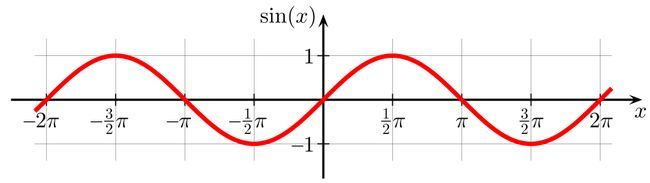 If the arc length for a full period of sine function can be written as
for positive integers
and
. Find
.
If the arc length for a full period of sine function can be written as
for positive integers
and
. Find
.
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Well, the problem could have been better but still a nice one.
What is arc length? One can see that it must be a line integral like - ∮ d s . Now what's d s ? It is the line "fragment" for our arc length i.e. ( d s ) 2 = ( d x ) 2 + ( d y ) 2 , by Pythagoras Theorem.
We can thus change our integral to
∫ a b 1 + ( d x d y ) 2 d x for some limits a and b .
For our function y = s i n ( x ) over x = 0 to x = 2 π ,
Arc Length = ∫ 0 2 π 1 + c o s 2 ( x ) d x
This is of the form of an elliptic integral and more specifically here .
So,
Arc Length = 4 2 E ( 2 1 )
which becomes
2 π Γ ( 4 1 ) 2 8 π 2 + Γ ( 4 1 ) 4