Sinful area
The total area enclosed by the elephant below is 4.
Now we form a new shape by joining two of the original elephants after shrinking them widthwise by a factor of two (as shown below). Is the area enclosed by these elephants also 4?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
11 solutions
Moderator note:
This principle can apply with calculus problems involving more traditional formulas. For example, compare the area under the curve f ( x ) = cos ( x ) + 1 from 0 to 2 π to the integral under the curve f ( x ) = cos ( 2 x ) + 1 from from 0 to 2 π :
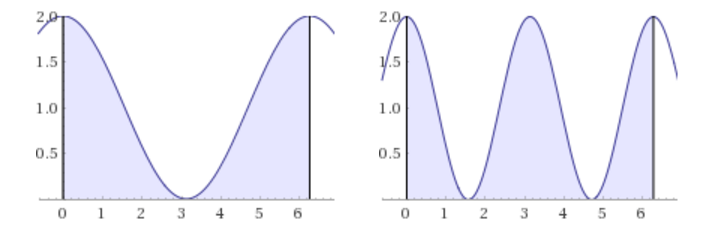
Both of them have the same area, 2 π !
Thank you foy your answer :) . This solution is based to the basic idea of calculus that to calculate an area you have to add an infinite number of infitensimaly small areas like the areas of these squares. It is not necessary to be squares. I could give it with the rigorous integral picture but i wanted to give the primitive thought under all of these. One argument could be that i can consider the triangles again as a sum of squares but to show you triangles work : imagine small triangles of height H and basis B then for the initial triangle the area is A=1/2 H B. After the transformation i have 2 triangles with basis B/2 so for each one of them the area is 1/2 H B/2 . But i have two of them so the new area is A'=2x (1/2) H B/2 = A . So triangles work too. I think you did a mistake to the transformation.You transormed only one of the side lenghts. In the triangle you cannot do that, and thats the reason i used the squares to make it more clear. In your case of the 2,2,2 triangle the initial height is 3 so the new triangle should have this height also.But at 2,2,1 has height 1 5 / 2 .
Also to show the solution to the elephant (or any shape) problem with the integrals. Suppose in general you have two random functions f ( x ) , g ( x ) defined at the domain [ a , b ] with f ( a ) = g ( a ) and f ( b ) = g ( b ) . Then you have the area to be A = ∫ a b ( f ( x ) − g ( x ) ) d x . And changing the variable x to y = x / 2 you see that you have A = 2 ∫ a / 2 b / 2 ( f ( 2 y ) − g ( 2 y ) ) d y so in terms of integral language this transformation is just a change of the variable that expresses the exact same integral. Notice also that the condition that the functions meet at the ends is not needed, it applies in general as Pi Han Goh also pointed out.
I think there is a flaw in this argument. This procedure of using squares to approximate the elephant could be used on any shape, right?
Let's take a triangle with side lengths 2, 2, 2 for example. It has an area of approximately 1.73 (https://www.wolframalpha.com/input/?i=2,2,2+triangle)
Maintaining height and halving the width leaves us with a triangle with side lengths 2, 2, 1. This has an area of approximately 0.97 (https://www.wolframalpha.com/input/?i=2,2,1+triangle)
2*0.97 = 1.94 > 1.73, so after shrinking and doubling the area is not the same.
I would say that a shape transformed as in the task only has the property of maintaining area if the area is calculated by width * height. Having a very complex shape, I believe that after the transformation, the elephants will not have the same area as before. (please correct me if I made a mistake:)
Log in to reply
That's not quite what the solution is saying, but I personally like to think about it like that. However, the key insight when approaching it your way is to realize that the elephant always takes up the same fraction of the square, regardless of the dimensions of the square, and this is true of any shape. For example, a circle in a square will always take up pi/4 parts of the area, no matter what the size of the square is.
Also, note that the problem with your triangle argument is that halving the width of a 2-2-2 triangle won't give you a 2-2-1 triangle, but rather something closer to a ~1.8-1.8-1 triangle.
It is hard to imagine the elephant as an union of squares!
Relevant wiki: Length and Area Problem Solving
the previous area and the new formed area is same.
just look carefully------the previous height and the new formed height is same....[for height]
and..the width of a new formed elephant is 2 1 of the previous elephant.so, the width of the 2 elephant will be
2 1 + 2 1 = 1 or same of the previous width......[for width]
as, width and height both are same,the area must be same.
It doesn't satisfied
I thought that one of the elephant using its trunk to catch tail of other will cause a slight reduction in area.
Sorry, this won't work. Assume the first elephant is the shape of an elipse. In the second iteration, the elephant elipse has the same vertical value and half the horizontal value, maintaining the same area for the box containing the elephants. Repeat this an infinite number of times. With each iteration, the area not covered by the elephant shapes shrinks. Ultimately, as the horizontal value approaches but does not reach zero, the elipse approaches rectangularity and the area not covered by replicating elipitcal elephants approaches zero. QED.
Log in to reply
Actually, that isn't what happens as the elephants gets smaller and smaller. Suppose our elliptical elephant has semi-axes of length h , l , where h is along the height and l is along the width. The area of the ellipse is equal to h l π . Suppose now we create n copies of the ellipse whose width are shrunk by a factor of n . Then, we have n ellipses with axes h , n l . The sum of the areas of all of these ellipses is equal to n ( h ) ( n l ) π = h l π , which was the same as the original ellipse. Since this value for the area does not depend on n , it doesn't matter if we have 2, 5, 100000, or infinitely many copies of the elephant: the area will always remain the same no matter what.
Relevant wiki: Area of a Rectangle
Elephant's height: X
Width: Y
XY = 4 ---------- Imagine the elephant as a rectangle figure.
1 half elephant = X ( 2 Y ) = 2 X Y = 2 4 = 2
There are two of the elephants, so 2*2 = 4
Yes, it is 4
with rectangles it's a lot more obvious. The hard part of the problem is understanding the shape of the elephant doesn't matter, and that its area is halfed when it's shrinked with a factor of 2.
I have a circle with diameter 10 cm. I halved its so called width, which is now 5 cm. And length is 10 cm, its original radius. If I put two of the modified circle, will it be ever equal to the original circle? I think this can also apply here.
But the question is, does the fact still hold even though the elephant is not a rectangle?
Log in to reply
Yes, like Maxime Weill wrote, "Its area is halfed when it's shrinked with a factor of 2."
Draw a rectangle around the elephant so that the elephant fits snugly inside i.e. the rectangle cannot be made any smaller without having it overlap with the elephant.
When we shrink the elephant widthwise by a factor of 2, the width of the rectangle will also get shrunk by a factor of 2. This type of transformation is called a distortion . Distortions preserve ratios of areas, so we can say that
Area of rectangle Area of original elephant = Area of shrunken rectangle Area of shrunken elephant .
The area of the shrunken rectangle will be one-half of the area of the original rectangle, so
Area of original elephant Area of shrunken elephant = 2 1 .
Thus, the area of the shrunken elephant is exactly half of the original elephant. Since we have two of these shrunken elephants, the total area is equal to the area of the original elephant. We conclude that yes , the area will be exactly 4.
Addendum : This method of inscribing a figure inside of a rectangle can be used to show that the area of an ellipse with semi-major and semi-minor axes a , b , respectively, is equal to a b π .
Since the width was halfed, on the second diagram e2 and e3 both are half of the first elephant(e1). a1 = h1×w1 (the first diagram ) a =h1 (w2+w3)--- w1 + w2 =[(1/2)w2 (1/2)w3] =(1)w1 & h1= h2 Therefore, a1 = a [h1×w1= h1×w1]= 4
If we half the width...area becomes half... Now two half widthed areas make the original area... (Do not consider the shape of elephant...it is the area that matters)
If we have a first area a 2 , than with half width: a × 2 a = 2 a 2 . So we have half of the area. 2 × 2 a 2 = a 2 . So, the correct answer is Yes, it is 4 .
Both figures had the same area as the original elephant, but when we halved each or their widths, their halves formed one whole width!
Divide the 2D figure...... Into lots of infinetisimally small squares..... (no. Of squares =n (say.... A very large no.)
Each squares having sides as 'h'(say) . Total area =n (h h)..........(i.e =4)
For the 2nd figure.... Total area of each part=n* (h*(h/2))
Therefore finally total area remains same. :)
The only hesitation I had was whether the tip of the trunk and the tip of the tail overlapped. Otherwise it's clear that this is an algebraic transformation, 2 a ∗ 2 = 1
It doesn't matter what size or shape the shape is. Once it's area has been shrunken by a factor of two (half), it is 2 1 of it's original size. However, if you join two of the same shrunken shapes together, it will be the size of the original shape.
Relevant wiki: Length and Area Problem Solving
Imagine the elephant as a sum of many many very small squares, so that the sum of their area is approximantely the sum of the tiny squares areas. If we magnify and look only at one square when we do the transformation of: Height-> Height , Width-> Width/2 then we see the area is preserved.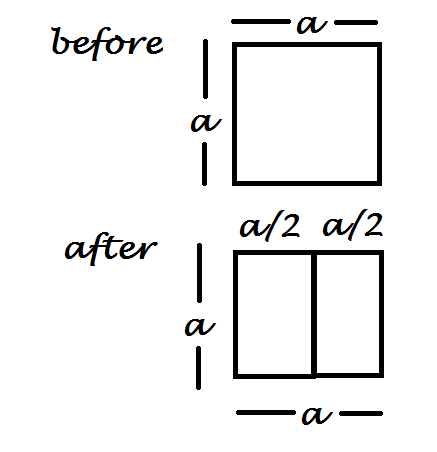 So if we sum the area of the new squares we get the same area with the initial elephant.
So if we sum the area of the new squares we get the same area with the initial elephant.