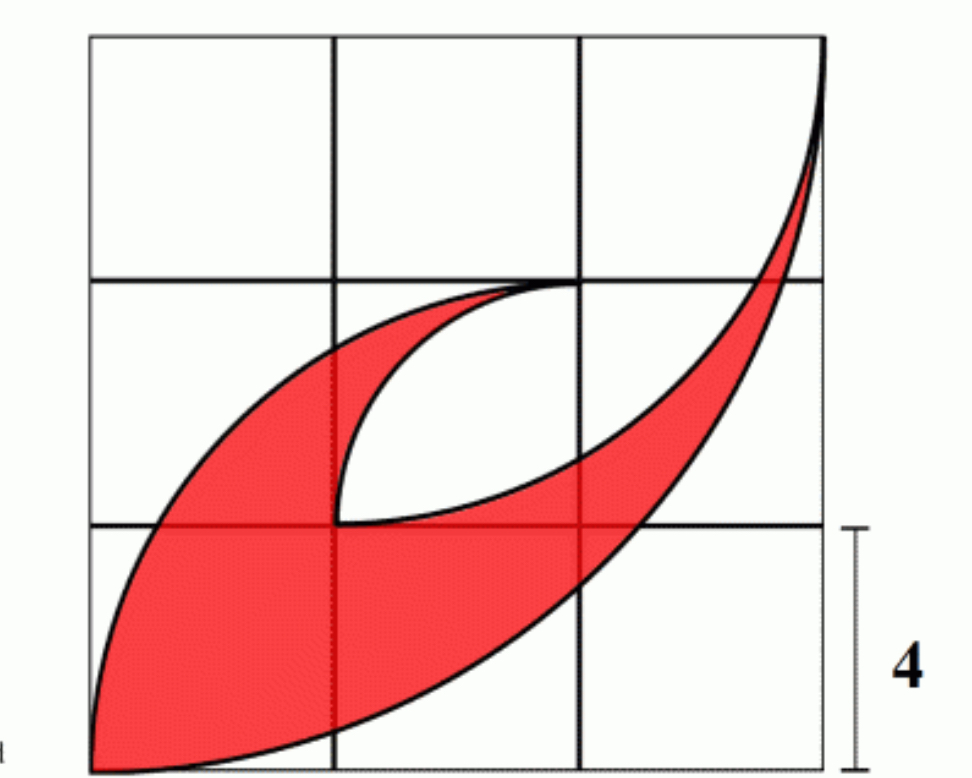
Singapore Geometry Problem.
The red region in the diagram is enclosed by 4 quarter-circles. What is its area?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
For excitement, I am gonna leave the actual solving to the reader, for I believe he/she already knows how to solve the area of a circle.
I am just gonna show my steps in a visual way, adding and subtracting areas along the way.
-
Step 1: Add
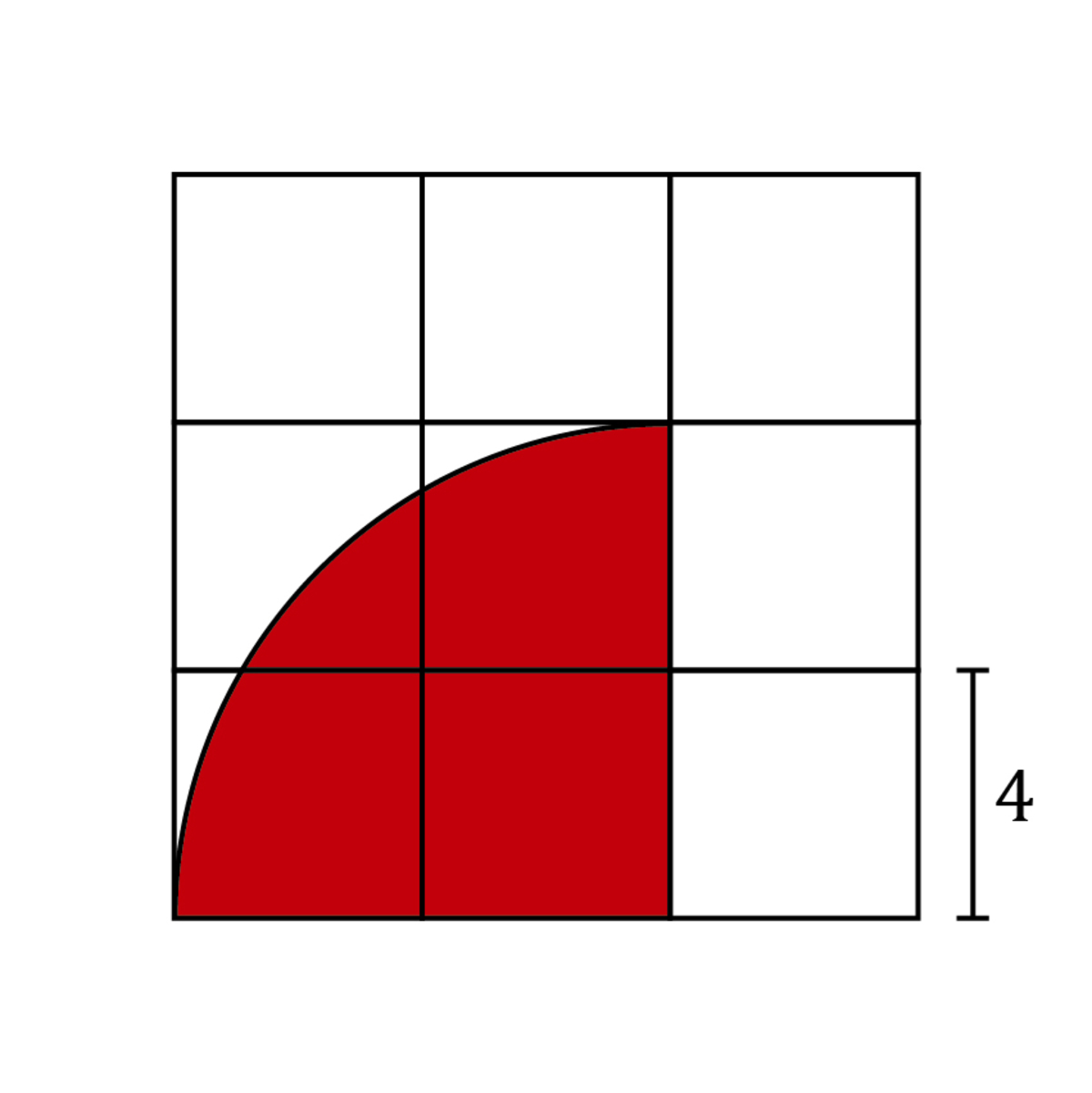
-
Step 2: Subtract
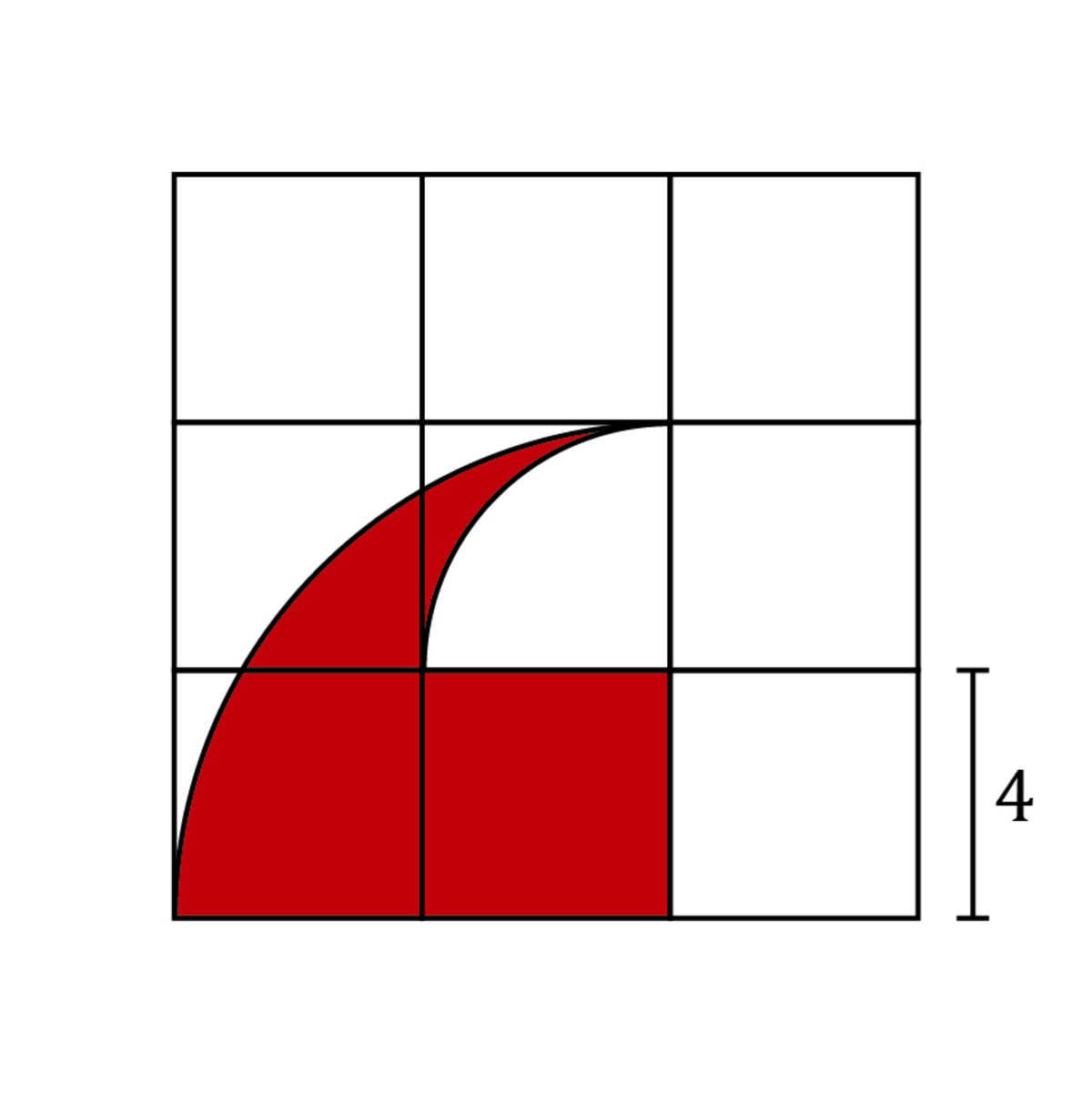
-
Step 3: Add
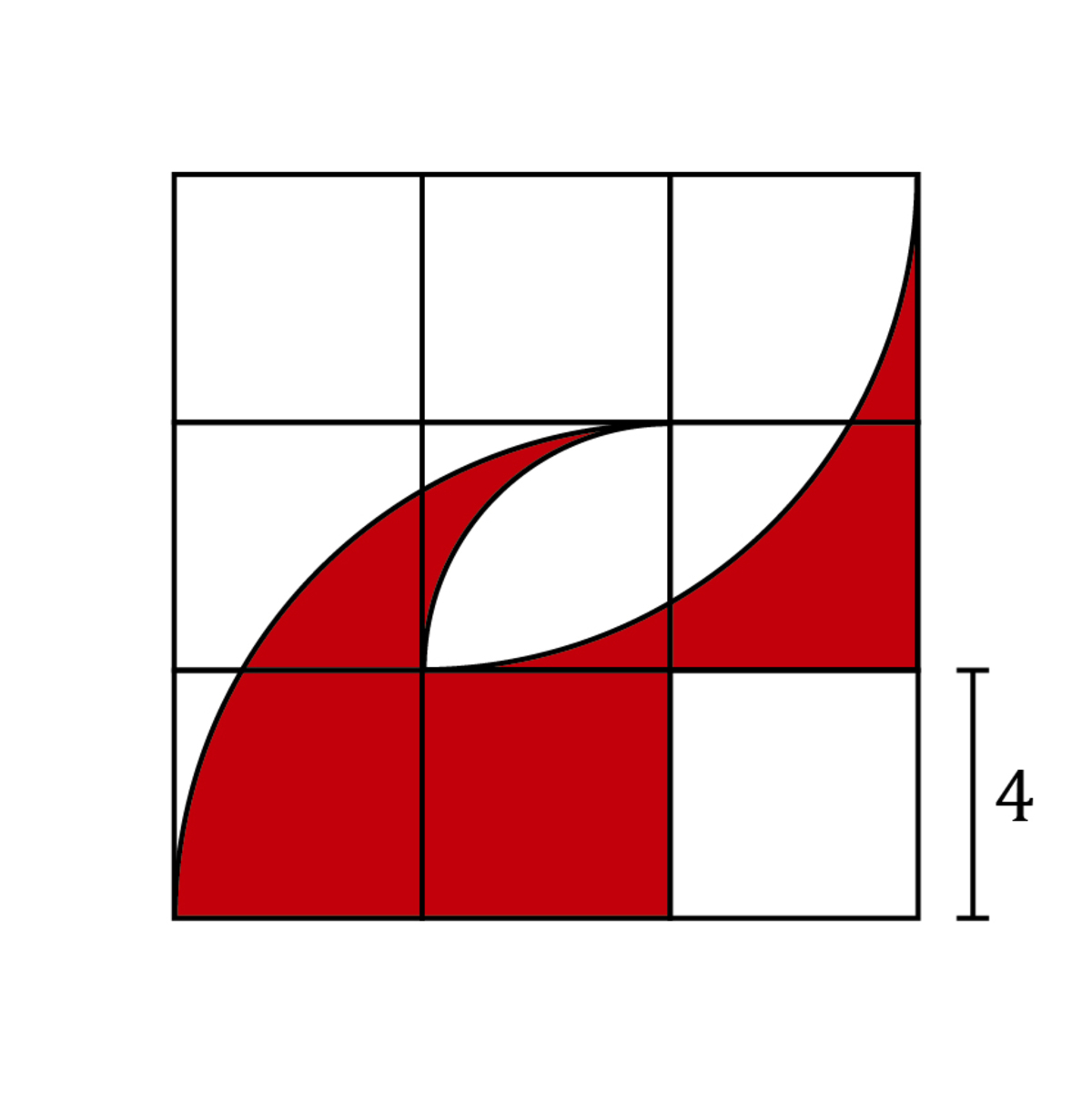
-
Step 5: Add
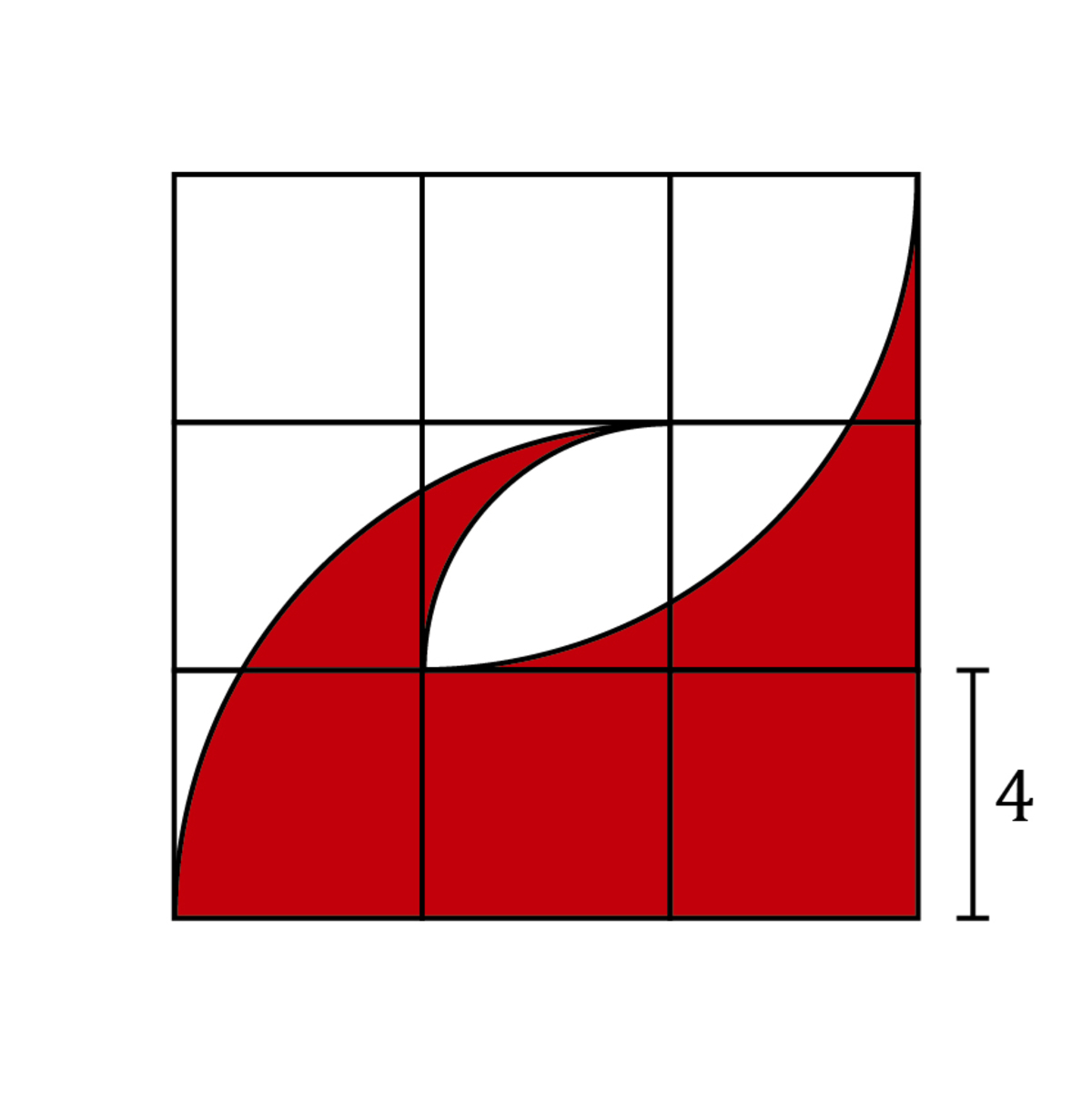
-
Step 6: Subtract
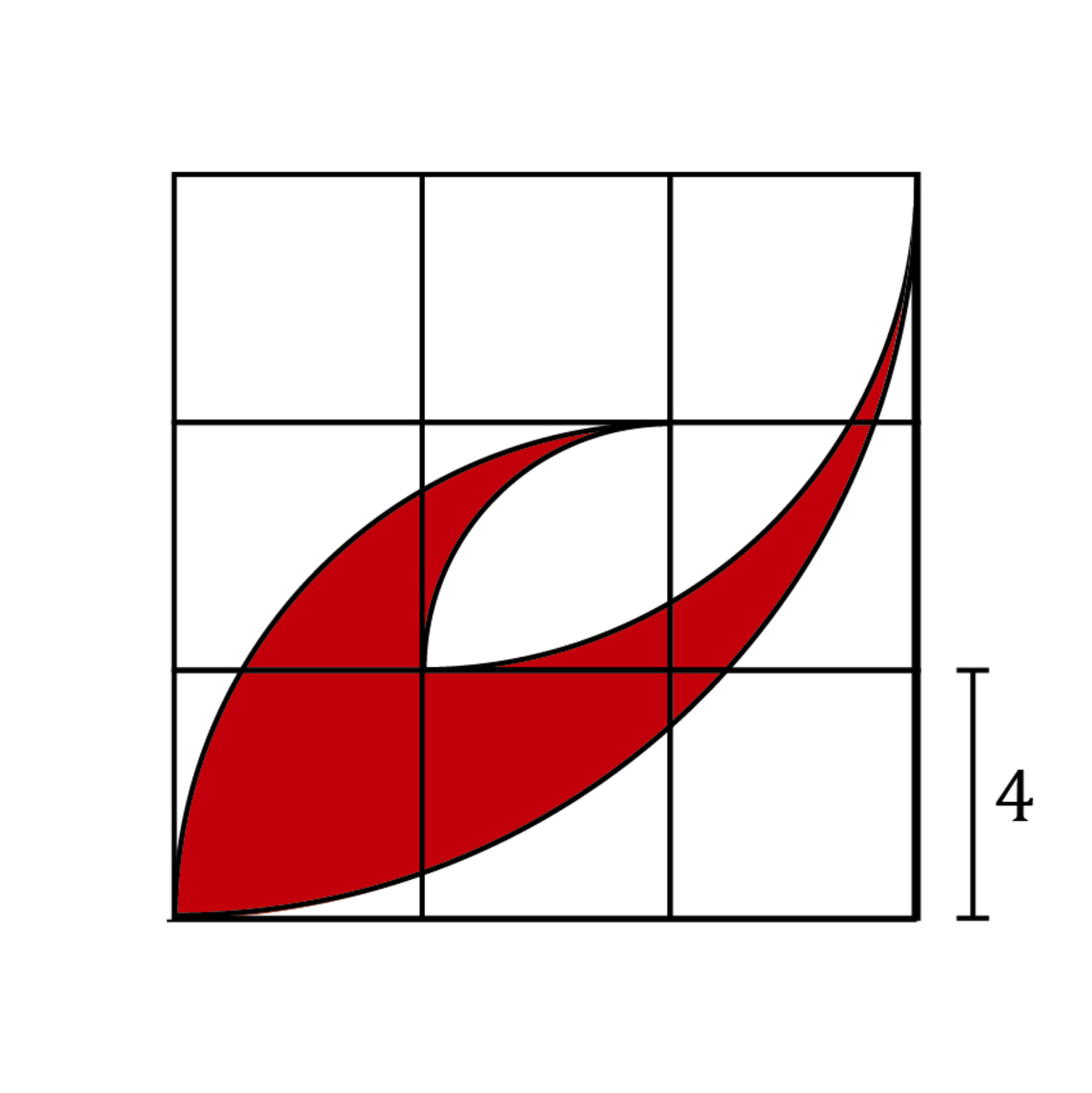
The problem becomes level 1 when approached this way.
From step 3 to step 5? ThE pRoBlEm BeCoMeS lEvEl 1
Define the following shape as
M
k
, where k is the dimension(s) shown.
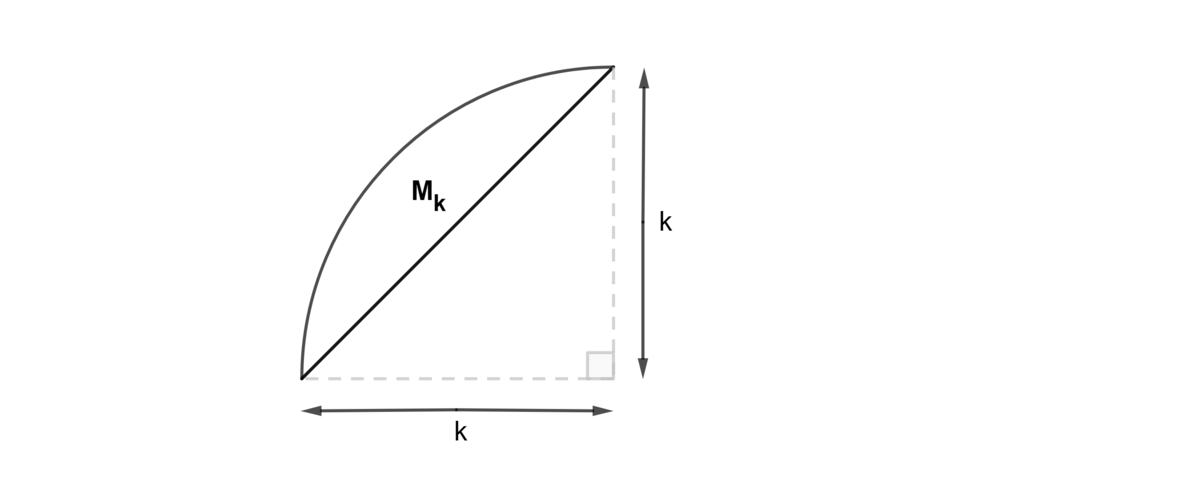 Let
A
k
be the area of
M
k
; then clearly
A
k
is
4
π
k
2
−
2
k
2
.
Let
A
k
be the area of
M
k
; then clearly
A
k
is
4
π
k
2
−
2
k
2
.
We draw a diagonal line to split the region (sorry, couldn't figure out how to get Geogebra to shade this) as shown below.
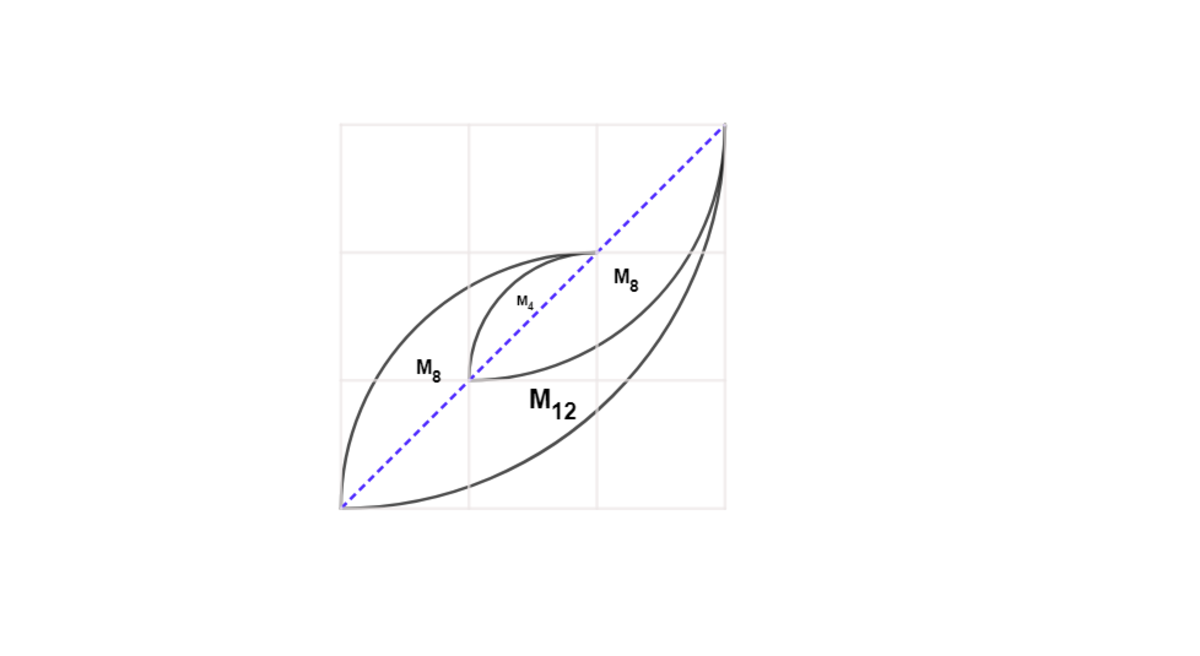 Then the area of the part of the region above the diagonal line is
A
8
−
A
4
. Similarly, the area of the part of the region below the diagonal line is
A
1
2
−
A
8
. Thus the total area is
(
A
8
−
A
4
)
+
(
A
1
2
−
A
8
)
=
(
A
1
2
−
A
4
)
=
(
4
π
(
1
2
)
2
−
2
1
2
2
)
−
(
4
π
(
4
)
2
−
2
4
2
)
=
(
3
6
π
−
7
2
)
−
(
4
π
−
8
)
=
3
2
π
−
6
4
Then the area of the part of the region above the diagonal line is
A
8
−
A
4
. Similarly, the area of the part of the region below the diagonal line is
A
1
2
−
A
8
. Thus the total area is
(
A
8
−
A
4
)
+
(
A
1
2
−
A
8
)
=
(
A
1
2
−
A
4
)
=
(
4
π
(
1
2
)
2
−
2
1
2
2
)
−
(
4
π
(
4
)
2
−
2
4
2
)
=
(
3
6
π
−
7
2
)
−
(
4
π
−
8
)
=
3
2
π
−
6
4
https://www.youtube.com/watch?v=B_yNI3gAHNk
First Solution:
Second Solution :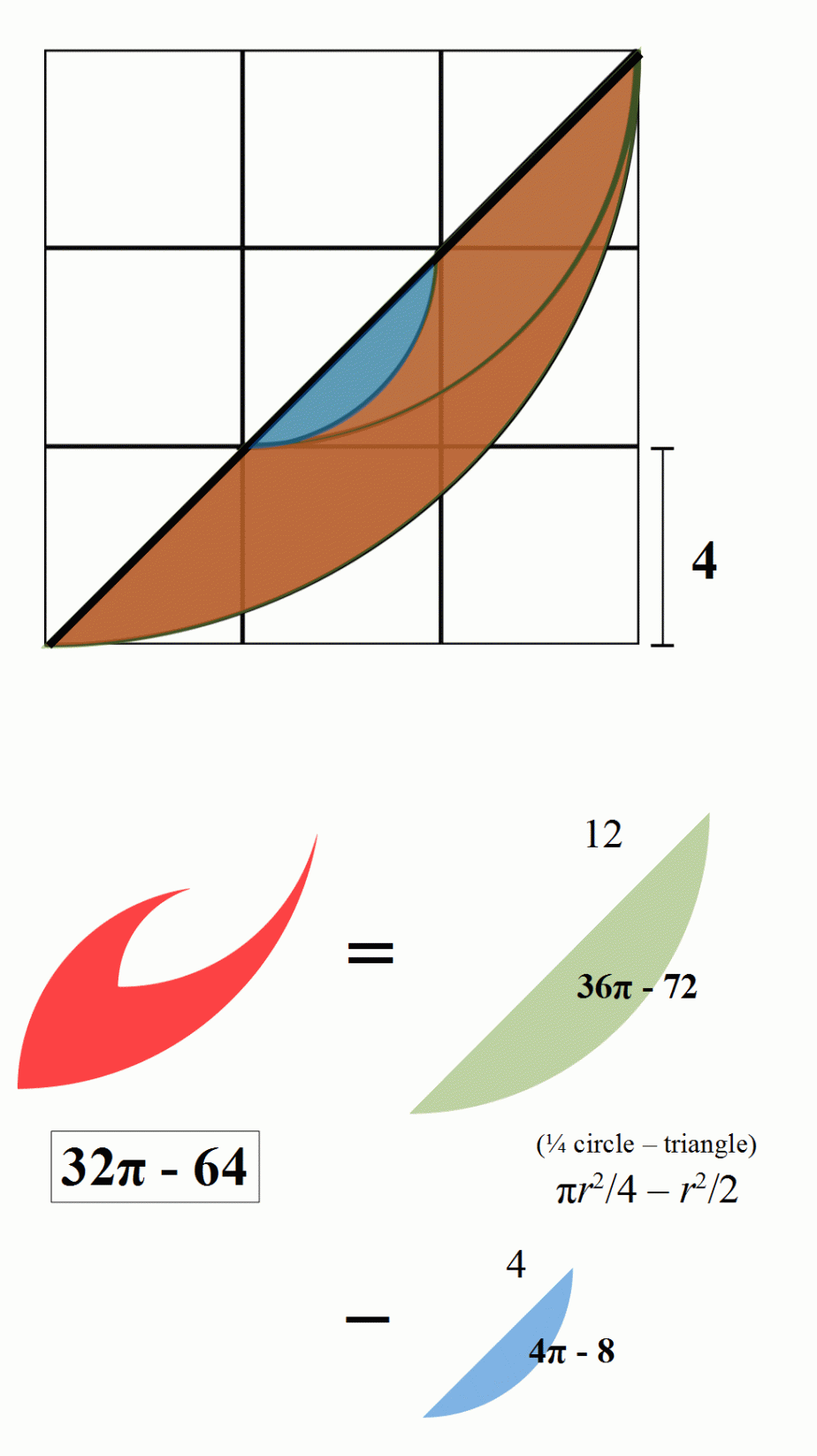
The above solutions are from this source: https://www.youtube.com/watch?v=yb_JUZFKi-A