Sins ain't bad

By the law of sines, $\frac{\sin A}{a} = \frac{\sin B}{b} = \frac{\sin C}{c} = \frac{2T}{abc} = k$ , where $T$ is the area of the triangle, and $k$ is a constant for that triangle.

Then $\sin A = ka$ , $\sin B = kb$ , and $\sin C = kc$ , and the ratio of the sides between a triangle with side lengths of $\sin A$ , $\sin B$ , and $\sin C$ to a triangle with side lengths $a$ , $b$ , and $c$ is $k$ , which means the ratio of the areas is $k^2$ .

Therefore, if $T_2$ is the area of the triangle with side lengths of $\sin A$ , $\sin B$ , and $\sin C$ and $T_1$ is the area of the triangle with sides lengths of $a$ , $b$ , and $c$ , $T_2 = k^2T_1$ . Since $k = \frac{2T}{abc}$ , $T_2 = \frac{4T_1^3}{a^2b^2c^2}$ .

In this problem, we can let $a = 5$ , $b = 4\sqrt{2}$ , and $c = 7$ . Since its area can be calculated by Heron's formula to be $T_1 = 14$ , $T_2 = \frac{4(14)^3}{5^2(4\sqrt{2})^27^2} = \frac{7}{25}$ , and $7 + 25 = \boxed{32}$ .

Drop altitude BD and notice that CD = 3, AD = 4, and BD = 4. (Do you know how to show this?)
Then we can calculate that the area of the triangle is $\frac{1}{2} \times 7 \times 4 = 14$ , and $\sin A = \frac{1}{ \sqrt{2} }$ .
(It is a well known fact that) By using the law of sines, the new triangle is similar to the original triangle.
Since length $5$ is mapped to length $\frac{1}{ \sqrt{2} }$ , hence the area is $\left( \frac{1 } { 5 \sqrt{2} } \right) ^2$ of the original, which gives us $\frac{14}{50} = \frac{7}{25}$ .

We know from the law of cosines that $\cos A = \frac{5^2-(4\sqrt{2})^2-7^2}{-2*7*4\sqrt{2}} = \frac{-56}{-56\sqrt{2}} = \frac{\sqrt{2}}{2}$ , hence $\angle{A} = 45°$ and $\sin A = \frac{\sqrt{2}}{2}$ $(1)$

We know from the law of sines that $\frac{5}{\sin A} = \frac{4\sqrt{2}}{\sin B} = \frac{7}{\sin C}$ , hence from $(1)$ we have $\sin B = \frac{4\sqrt{2}\sin A}{5} = \frac{4}{5}$ and $\sin C = \frac{7\sin A}{5} = \frac{7\sqrt{2}}{10}$

Thus from Heron's formula, the area of a triangle whose side lengths are $\sin A, \sin B$ and $\sin C$ is $\sqrt{s(s-\sin A)(s-\sin B)(s-\sin C)}$

where $s = \frac{\sin A + \sin B + \sin C}{2} = \frac{5\sqrt{2}+8+7\sqrt{2}}{10} = \frac{3\sqrt{2}+2}{5}$ .

So the area is equal to $\sqrt{(\frac{3\sqrt{2}+2}{5})(\frac{\sqrt{2}+4}{10})(\frac{3\sqrt{2}-2}{5})(\frac{-\sqrt{2}+4}{10})} = \frac{7}{25}$ .

Thus $\frac{p}{q} = \frac{7}{25}$ and $p+q = 7+25= \boxed{32}$ .

Using the law of cosines with the following included angles:

$\angle{C} \implies \cos(C) = \dfrac{3}{5} \implies \sin(C) = \boxed{\dfrac{4}{5}}$

$\angle{A} \implies \cos(A) = \dfrac{1}{\sqrt{2}} \implies \sin(A) = \boxed{\dfrac{1}{\sqrt{2}}}$

$\angle{B} \implies \cos(B) = \dfrac{1}{5\sqrt{2}} \implies \sin(B) = \boxed{\dfrac{7}{5\sqrt{2}}}$

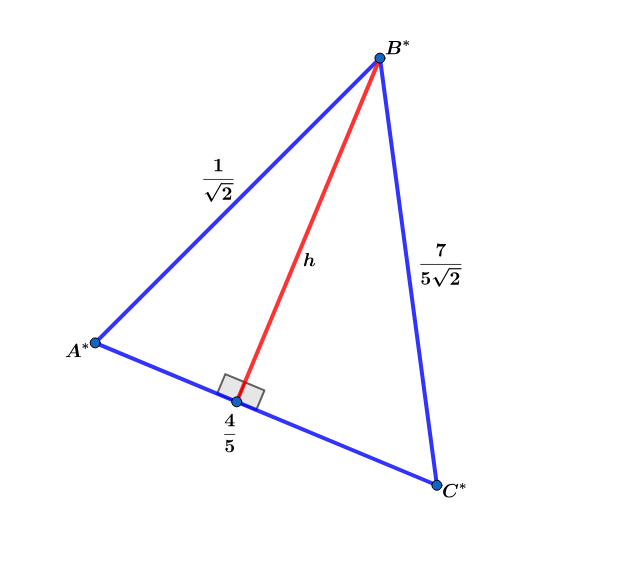
Using the law of cosines for the included angle $A^{*} \implies \cos(A^{*}) = \dfrac{1}{5\sqrt{2}} \implies \sin(A^{*}) = \dfrac{7}{5\sqrt{2}} \implies h = \dfrac{1}{\sqrt{2}}\sin(A^{*}) = \dfrac{7}{10}$

$\implies A_{\triangle{A^{*}B^{*}C^{*}}} = \dfrac{1}{2}(\dfrac{4}{5})(\dfrac{7}{10}) = \dfrac{7}{25} = \dfrac{p}{q} \implies p + q = \boxed{32}.$

Let $T$ be the area of $\Delta ABC$ and $t$ be the area of the other triangle.

By the Law of Cosines,

$\left(4\sqrt{2}\right)^2=5^2+7^2-2(5)(7)\cos{C}$

$\implies\cos{C}=\frac{3}{5}\implies\sin{C}=\frac{4}{5}$

Then by the Law of Sines,

$\dfrac{5}{\sin{A}}=\dfrac{7}{\sin{B}}=\dfrac{4\sqrt{2}}{\frac{4}{5}}=5\sqrt{2}$

which implies that all three sides of $\Delta ABC$ are $5\sqrt{2}$ times as big as those of the other triangle.

And since $\text{area}\propto\left(\text{length}\right)^2$ , if side lengths shrink by a factor $5\sqrt{2}$ , area would shrink by a factor of $\left(5\sqrt{2}\right)^2$ , or $50$ .

Thus, $t=T\cdot50^{-1}$ , and since

$T=\frac{1}{2}(5)(7)\left(\frac{4}{5}\right)=14$

we find that $t=\frac{14}{50}=\frac{7}{25}$

And finally, the value we seek is the sum of the numerator and denominator, i.e. $32$ .

First, use Heron's formula to calculate the area of the bigger triangle: $\sqrt{s(s-a)(s-b)(s-c)}$ where $s$ is half the perimeter of the triangle and $a, b,$ and $c$ are the sides of the triangle. We get that the area of the triangle is $14$ . Then, we can calculate some heights to find the sines of the angles. For the height dropped from $C$ to $AB$ , we get $\frac{14}{\frac{1}{2}\ 4\sqrt{2}}$ $=$ $\frac{7\sqrt{2}}{2}$ . And for the height dropped from $A$ to $CB$ , we get $\frac{14}{\frac{1}{2}5}$ $= 5.6$ . With these, we can calculate the sines of the angles: $\sin A$ $=$ $\frac{\sqrt{2}}{2}$ , $\sin B$ $=$ $\frac{7\sqrt{2}}{10}$ , and $\sin C$ $=$ $\frac{56}{70}$ . Now, we need to use Heron's formula on the little triangle. After doing so, we get that the area is $.28=\frac{7}{25}$ . The answer is then $\boxed{32}$ .

Let $T$ be the area of triangle $ABC$ , and $T^*$ the area of the smaller triangle. By Sine Law the two triangles are clearly similar; also, by applying Heron's Law, or by noticing that triangle ABC is composed of a $\ 3 \ \text{-} \ 4 \ \text{-} \ 5 \$ right triangle and a $\ 4 \ \text{-} \ 4 \ \text{-} \ 4\sqrt{2} \$ right triangle attached at their sides of length $4$ , we have that $\ T=14$ .

In the diagram on the left, just like in the standard derivation of the Sine Law, we see that

$\begin{aligned} b \sin A = a \sin B &= h \qquad \qquad \small \text{[Divide by } ab] \\ \\ \dfrac{\sin A}{a} = \dfrac{\sin B}{b} \left( = \dfrac{\sin C}{c} \right) &= \dfrac{h}{ab} \\ \\ &= \dfrac{hc}{abc} \\ \\ &= \dfrac{2T}{abc} \\ \end{aligned}$

Now, applying the triangle area formula $\dfrac{1}{2} \alpha \beta \sin \Gamma \$ to the smaller triangle, we get that $2 T^* = \sin A \sin B \sin C^* = \sin A \sin B \sin C$ . Then,

$\begin{aligned} \dfrac{2 T^*}{abc} &= \dfrac{\sin A}{a} \cdot \dfrac{\sin B}{b} \cdot \dfrac{\sin C}{c} \\ \\ &= \left( \dfrac{2T}{abc} \right)^3 \\ \\ &= \dfrac{8T^3}{a^3b^3c^3} \\ \\ T^* &= \dfrac{4T^3}{a^2b^2c^2} \\ \\ &= \dfrac{4(14)^3}{25 \cdot 32 \cdot 49} \\ \\ &= \dfrac{7}{25} \end{aligned}$

and our answer is $7 + 25 = \boxed{32}$