Six Lines, Six Sides, One Point
 ⎩
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎧
a
+
b
a
+
c
a
+
e
2
a
=
=
=
=
c
+
e
e
c
+
d
e
+
f
⎩
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎧
a
+
b
a
+
c
a
+
e
2
a
=
=
=
=
c
+
e
e
c
+
d
e
+
f
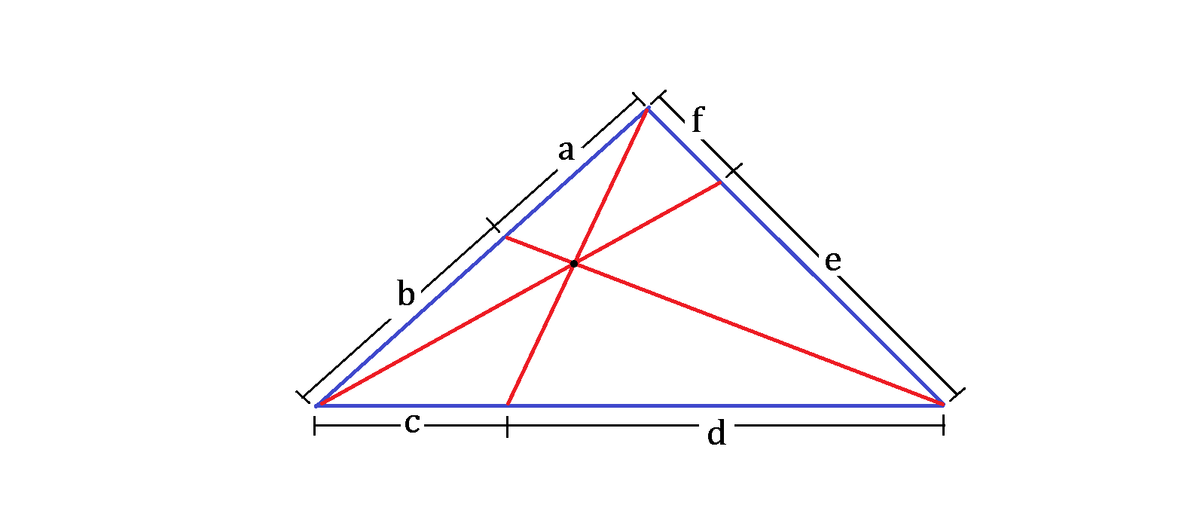
A triangle has three side lengths of co-prime integers. Then the lines are drawn from the vertices, passing one common point, to the opposite sides, dividing into 6 lengths a , b , c , d , e , f , satisfying the constraints above.
What is the perimeter of this triangle?
The answer is 34.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Good usage of ceva's theorem to set up the concurrency constraint.
Log in to reply
Thank you. A little bit hard to come up with these co-prime stuff though. 😉
None of the constants is 0.
a+b = c+e ........(1)
a+c = e ........... (2)
a+e = c+d ...... (3)
2a = e+f ......... (4)
(1) - (2)...gives ......................b=2c ...........(5)
(2) + (3).gives ......................d=2a ............(6)
By Ceva's Theorem,
a * c * e = b * d * f
From (5) and (6),
a * c * e =2c * 2d * f
So e = 4f,
By (4) e + f = even.
So likely ................f = 2, ...e = 8.
From (4) ................a = 5.
From (2) ................c = 3.
From (5) ................b = 6.
From (6) ................b = 10.
The sides are ,
5+6=11,......3+10=13,........8+2=10.
They are co-prime and integers.
So perimeter = 11 + 13 + 10 = 3 4
a + b = c + e ( 1 )
a + c = e ( 2 )
a + e = c + d ( 3 )
2 a = e + f ( 4 )
From the first and second constraint, we can conclude: b = 2 c
From the second and third constraint, we can conclude: d = 2 ( e − c ) = 2 a
Then according to Ceva's theorem , b a ⋅ d c ⋅ f e = 1 .
Thus, 2 c a ⋅ 2 a c ⋅ f e = 1 .
Hence, e = 4 f .
Referring to the fourth constraint, 2 a = 5 f ,
Thus, a = 5 k and f = 2 k for some positive integer k .
Then e = 4 f = 8 k .
d = 2 a = 1 0 k .
c = e − a = 8 k − 5 k = 3 k .
Finally, b = 2 c = 6 k .
Then a + b = 1 1 k ; c + d = 1 3 k ; e + f = 1 0 k .
Since all the three sides of this triangle are co-prime, k = 1 .
As a result, the perimeter equals a + b + c + d + e + f = 5 + 6 + 3 + 1 0 + 8 + 2 = 3 4 .