Sketch it
Drawn from the origin are two mutually perpendicular straight lines forming an isosceles triangle with the straight line . Then the area of triangle is . Find .
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
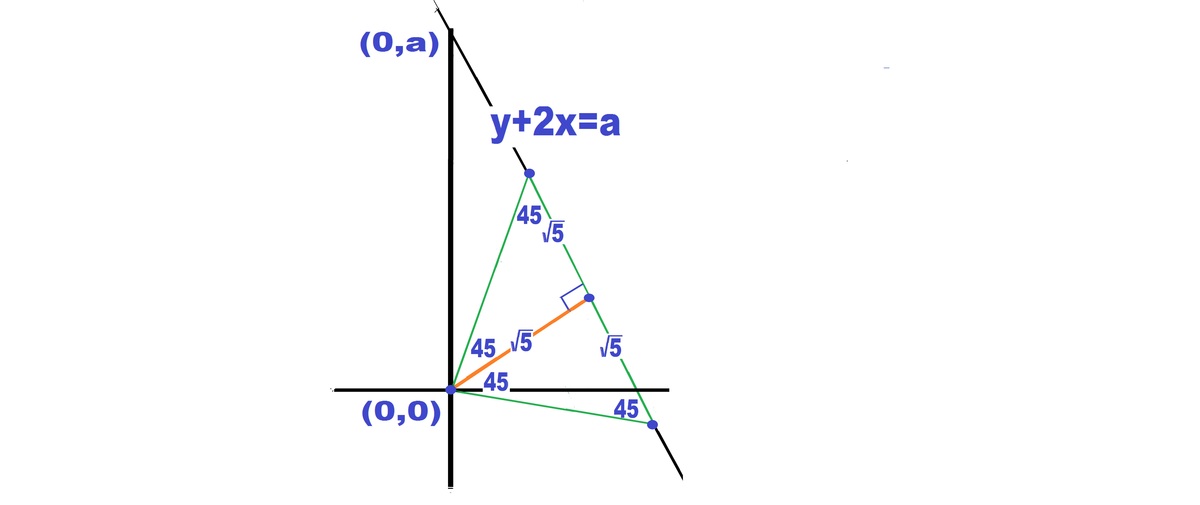The triangle is a 45-90-45 triangle. The distance of the line from (0,0) is
5
. So this is the altitude from the 90 degree vertex. So area is
a
2
/
5
. Therefore
T
a
n
2
(
6
0
∗
5
)
=
3
assuming the angle is in degrees. That only is possible . ...........
Sorry
for making a report because of my misunderstanding.