Sketching Curves 2

Calculus Level 2

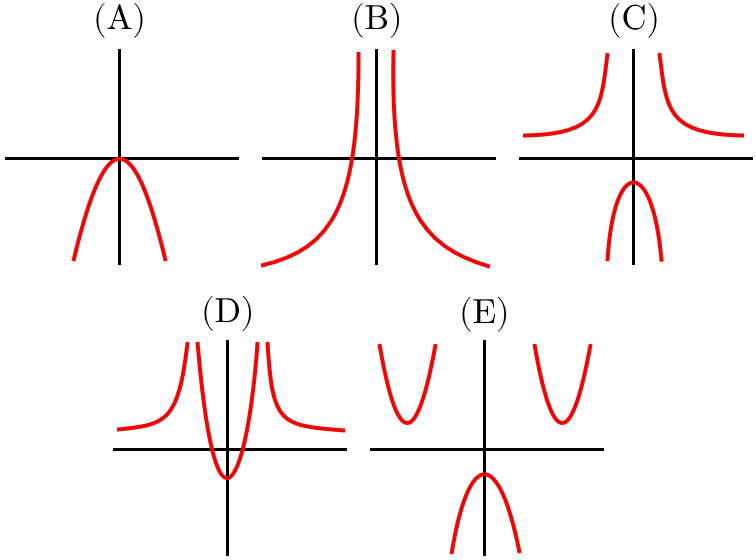
The graph of the function $y=\dfrac{x^2+1}{x^2-1}$ is sketched in which set of axes?

Like this? Try Sketching Curves 1 .

A B C D E

4 solutions

Domenico Franceschelli
Feb 1, 2016

This is how I solved it with 2 steps only:

There are no values of x for which f(x) = 0, so the function never crosses the x axis. This leads us to eliminate A, B and D.
The derivative (f'(x)) of the function is f'(x) = -4x / (x^2 -1)^2, and it's easy to notice that we have f'(x) > 0 for x<0, and f'(x)<0 for x>0. This tells us that the function increases for x<0 and decreases for x>0. So the correct representation of the function must be C.

Jacob Standa
Jan 29, 2016

To sketch curves, it helps to find the asymptotes, maximums, and minimum points. Finding the vertical asymptotes requires setting the denominator to zero, as at that point the function does not exist.

x^2 - 1 = 0 x^2 = 1 x = ±1

Thus the function has asymptotes at x = 1 and x = -1, eliminating options A and B.

To obtain maxes and mins requires obtaining the derivative of y, since a maximum or minimum point will be where the tangent slope is 0. Setting the derivative to zero will give the x-values of where the tangent line will equal zero.

y = x^2 + a/x^2 - 1

Using the quotient rule:

y' = 2x(x^2 - 1) - 2x(x^2 + 1) / (x^2 - 1)^2

Factoring 2x from the numerator

y' = 2x(x^2 - 1 - x^2 - 1) / (x^2 - 1)^2

And simplifying the numerator.

y' = 2x(-2) / (x^2 - 1)^2 = -4x / (x^2 - 1)^2

Now setting the derivative to zero to find the x-value of the maxes and mins:

-4x / (x^2 - 1)^2 = 0

-4x = 0

x = 0

Thus the graph must have a max or min at x = 0, but no where else, eliminating option E. To finish sketching the graph, it must be known whether at x = 0 there is a max or a min. To do so requires the direction of the slope just before and just after the max or min. At a max, the slope before will be positive and the slope after will be negative. Since the derivative gives the slope of the tangent, plugging in x values just before and after x = 0 into the derivative will yield the slopes before and after x = 0.

Given the derivative y' = -4x / (x^2 - 1)^2 , a positive value will yield a negative slope and a negative value will yield a positive slope (no plugging in is necessary). Thus, the function has a positive slope before x = 0 and a negative slope after x = 0, meaning there is a maximum at x = 0. This leaves only option C.

The equation can be written as $y=1+\frac{2}{x^2-1}$ so $y=1$ is a horizontal asymptote, also notice that as $x\rightarrow \pm \infty$ $y\rightarrow 1^+$ . $x=\pm 1$ are vertical asymptotes, and the y-intercept is $-1$ also there are no x-intercepts. Based on these observations the only curve possible is $\boxed{C}$

Yasir Soltani - 5 years, 4 months ago

Pete Markou
Feb 1, 2016

It tends to 1 as x goes to infinity. So it is either C or D. For y=0 there are no solutions, so it never crosses the x axis. Therefore C.

Harish Sasikumar
Feb 1, 2016

Solved it by elimination.

The graph cannot cross or touch x axis (For any x, y cannot be zero). Hence A, B or D cannot be the answers.
y tends to 1 when x tend to infinities (+ or -). Hence E cannot be the answer.
The remaining option C is the answer.

Sketching Curves 2

Like this? Try Sketching Curves 1 .

4 solutions

0 pending reports