Ski jumping
A ski jumper launches from a ski jump that is oriented parallel to a hill. The jump has a vertical drop of 50 m and the coefficient of friction μ between the skier and the jump is 0.05. The launch point is 5 m above the hill and there is a small lip at the bottom of the jump so that the skier launches horizontally. How long in seconds is the skier in flight?
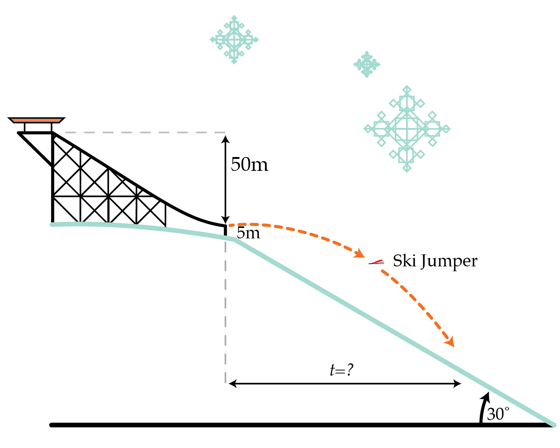
Details and assumptions
- Neglect air resistance.
- The acceleration of gravity is − 9 . 8 m / s 2 .
- The hill slopes down at an angle of θ = 3 0 o below the horizontal.
- The skier started from rest at the top of the jump.
The answer is 3.794.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Can you define your variables, please?
\noindent Let us split this scenario into two parts and analyse them separately to simplify matters:\
\begin{enumerate}
\item \textbf{Skiing on the slope} \item \textbf{Flying in mid-air (after launch)}\[5pt] \end{enumerate}
\noindent \mbox{\bfseries 1. Skiing on the slope}\[7pt] Before jumping straight into this part, let us look at part 2 briefly. Since we want to find the time t, it is logical that we should find the speed of launch (which we shall denote by $v$). The common and widely-used method to find $v$ is by conservation of energy.\[5pt] The initial energy that the skier has is his or her gravitational potential energy, $Mgh$. The final forms of energy the skier has (when he or she reaches the launching point) should be his or her kinetic energy, $\frac{1}{2}Mv^2$.\[5pt] However, the matter is not so simple. Since we are given the coefficient of friction $\mu$, we have to take the work done by the frictional force, $f$, into account. Thus, we get the equation below,
\begin{equation} Mgh=\frac{1}{2}Mv^2+fd \end{equation}
\noindent where $d$ is the distance (NOT displacement, since friction is a non-conservative force) travelled by the skier. We then note that the only unknown terms in the equation above are $f$ and $d$.\[5pt]
To find $f$, we use the relation $f=\mu N$, where $N$ is the normal force exerted by the ski slope on the skier. We then draw the free-body diagram to find $N$(since I haven't learnt how to draw diagrams in \LaTeX , I shall describe it in words).\[5pt]
The forces acting on the skier are friction, gravity (weight), and the normal force. Let us define the x and y planes as the planes parallel to and perpendicular to the surface of the ski slope respectively. Since $N$ is in the y-plane, we only need to care about the components of the other forces in the y-plane, which in this case, can only be that of gravity. Since there is no net acceleration in the y-plane, the net sum of the forces in the y-plane is zero. This means $N=Mg\cos 30^{\circ}$.\[5pt]
As for $d$, we realise that it is just the length of the ski slope. Hence, $d=h\csc 30^{\circ}$.\[5pt]
Now that the only unknown term in equation (1) is $v$, we can find $v$.\[7pt]
\noindent \mbox{\bfseries 2. Flying in mid-air (after launch)}\[7pt]
It should be clear that in this part, our kinematic equations come into play.\[5pt]
In the vertical direction, we have
\begin{equation}
\frac{1}{2}gt^2=5+m
\end{equation}
where $m$ is the vertical displacement of fall between the launch point and the point on the slope the skier impacts.\[5pt]
In the horizontal direction, we have
\begin{equation}
vt=n
\end{equation}
where $n$ is the horizontal displacement of fall between the launch point and the point on the slope the skier impacts.\[5pt]
Next, we realise that there is a trigonometric relation between $m$ and $n$. It is
\begin{equation}
m=n\tan 30^{\circ}
\end{equation}
After that, we substitute equation (4) into (2), then equation (2) into equation (3). We will get a quadratic equation with $t$ as the only unknown variable. It should be as follows:
\begin{equation}
\frac{\sqrt{3}}{2}gt^2-\sqrt{\left(100+5\sqrt{3}\right) g}\hspace{1mm}t-5\sqrt{3}=0
\end{equation}
Solving equation (5) should give us the value of $t$.
The net force on the skier on the ski jump parallel to the ski jump surface is a combination of the gravitation force and the frictional force,
\(F_{net}=mg(sin \theta - \mu cos\theta)\).
The net work done on the skier as he travels down the jump is W = F L where L is the length of the jump, L = 5 0 / s i n θ . By the work-energy theorem the skier launches horizontally from the bottom of the jump with a speed
v = ( 2 g h ( 1 − μ c o t θ ) ) 1 / 2 .
After the skier launches (and treating the launch point as x,y=0), the horizontal and vertical position of the skier are
x = v t , y = − 2 1 g t 2 .
The landing spot is on the line y = − x t a n θ − 5 , so we have a system of equations we can solve for t=3.794 seconds.
What are your variables?
Using the conservation of energy principle, the work done by friction must be equal to the change in the mechanical energy of the system (h = 50m, alpha = 30°),
2 1 m v 2 − m g h = − μ m g cos α sin α h
which implies
v = 2 g h ( 1 − μ c o t α ) .
During the fall, using parallel (x axis pointing 'downwards') and perpendicular (y axis pointing 'upwards') axes in respect to the hill, we can write down the variation of y with time as
y = y 0 + v sin α t − 2 g cos α t 2 .
Setting y = 0 and solving for t (h' = 5m),
t = g v tan α ( 1 + 1 + v 2 tan α 2 2 g h ′ ) = 3 . 7 9 s .
The net force on the skier on the ski jump parallel to the ski jump surface is a combination of the gravitation force and the frictional force, . The net work done on the skier as he travels down the jump is where L is the length of the jump, . By the work-energy theorem the skier launches horizontally from the bottom of the jump with a speed . After the skier launches (and treating the launch point as x,y=0), the horizontal and vertical position of the skier are ,. The landing spot is on the line , so we have a system of equations we can solve for t=3.794 seconds.
Note: ski jump is parallel to the hill, and therefore angled at 30°
First, let us find the velocity of the skier upon "launching". Since there is some friction between skier and ice, we have:
Δ E = A = − F f r ⋅ L
where L is length of the ski jump, which is L = H / s i n ( θ ) , H = 5 0 m and F f r = μ ⋅ m g ⋅ c o s ( θ )
Also, Δ E = E 2 − E 1 = 2 1 m v 2 − m g H , so for the velocity we have:
v 2 = 2 g H − 2 g H ⋅ μ / t g ( θ ) , which gives: v = 2 9 . 9 1 9 m / s
Now, the fun part. We should choose our coordinate system to be placed at the launch point, or at the impact point. Either will work in this case, and I will chose the impact point, just to demonstrate how it is done.
In this system, initial position is ( x o , y o ) , and initial velocity is ( − v o , 0 ) - only in x-direction, and the final position is ( 0 , 0 ) . Motions in x and y directions are mutually independent (since there is no air friction), so we have:
x = x o − v o t and y = y o − 2 1 g t 2
and at the moment of impact, ( x , y ) = ( 0 , 0 ) , so:
x o = v o t and y o = 2 1 g t 2
If you draw the impact point on the figure in the original figure, you should be able to see that: y o = x o ⋅ t g ( θ ) + h , where h = 5 m
Using the last three equations we get the following quadratic equation:
2 1 g ⋅ t 2 − v o t g ( θ ) ⋅ t − h = 0
which gives two solutions:
t 1 = − 0 . 2 6 9 s e c
t 2 = 3 . 7 9 4 s e c
First result would have had physical sense if the skier had been in flight even before the launch, which we know not to be true, so the final solution is: t = 3 . 7 9 4 s e c