Skinny Triangle
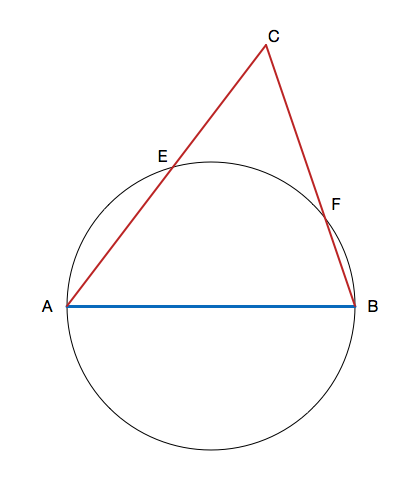Let
A
B
C
be a triangle such that
A
B
=
2
4
is the diameter of of a circle
O
. Points
F
and
E
lie on the intersection of the circle and lines
B
C
and
A
C
, respectively, such that
B
F
=
1
and
A
E
=
3
. Find the perimeter of triangle
A
B
C
. Round your answer to the nearest integer.
This problem was created while accidentally misinterpreting an OMO problem. :D
The answer is 311.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Here is an alternate solution using Intersecting Secant Theorem:
Let CE = x and CF = y
From Intersecting secant theorem:
CA . CE = CB . DF
i.e. x(x+3) = y(y+1) . . . . (I)
Now writing area of ABC in two ways using altitudes A F = 5 7 5 ; B E = 5 6 7 and bases
BC = (y+1) and AC = (x + 3)
we get ( x + 3 ) 5 6 7 = ( y + 1 ) 5 7 5 . . . . ( I I ) Solve I & II to get x = 8 3 × 5 6 7 − 8 5 6 7 × 5 7 5 = 1 4 1 . 2 5 2 Y = 142.245
Giving a perimeter of x +3 + y +1 + 24 = 311.497
Did the same but first I put in 312
There is an alternative solution using theorem of intersecting secants. I will try to post it separately.
We can also use ptolemy's theorem on the cyclic quadrilateral and find EF. Then use similarity ratios to get EC + CF ( triangle ECF ~ triangle BCA) So we can find the perimeter of the triangle.
R = 1 2 / ( ( 3 / 2 4 ) ∗ ( 2 4 2 − 1 ) / 2 4 + ( 1 / 2 4 ) ∗ ( ( 2 4 2 − 3 2 ) / 2 4 ) P = 2 4 + 2 R ∗ ( ( 2 4 2 − 3 2 ) / 2 4 + ( 2 4 2 − 1 ) / 2 4 = 3 1 1
An accurate calculation shows that the perimeter is 4 6 7 5 + 4 5 1 6 1 ≈ 3 1 1 . 4 9 6 , so the answer is actually 311.
Log in to reply
Thanks. I have updated the answer to 311.
Log in to reply
Thank you, btw, was the previous answer 312?
Sir, I got the answer as 311.52(rounded to 312, which was earlier correct )I had already used 2 tries and got the answer correct in 3rd try(due to some calculation mistakes). But now as the answer is changed to 311 my answer is incorrect, and since i had used all the tries i can't give the correct answer.Sir, I would request you if possible to provide another 3 attempts to those whose answer was correct earlier as there is very slight difference between the 2 answers.
oh, calculation mistake lost me points :(
FYI, the Latex for square root is \sqrt { }.
Can you explain how you arrived at those values?
Draw CH is perpendicular to AB. Because AB is the diameter of the circle O, so AF is perpendicular to BC, BE is perpendicular to AC. ∠ F A B = ∠ H C B , ∠ A C H = ∠ E B A ∠ A C B = ∠ F A B + ∠ E B A Apply sin theorem for triangle ABC, We have above formula.
a more accurate calculation shows 311.52
Relevant wiki: Power of a Point
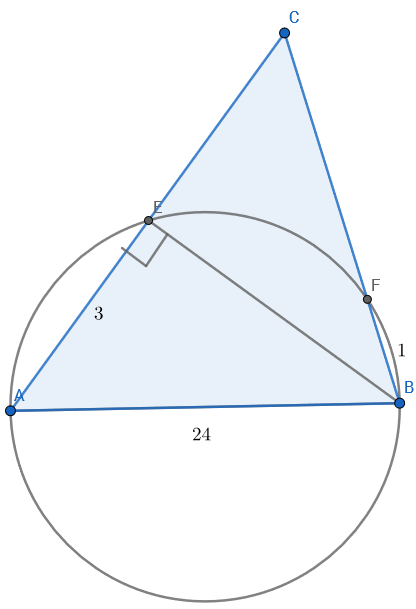
Let side A C = b ; B C = a
Construction:- Join B E .
Now, Since A B is the diameter, ∠ A E B = 9 0 ∘ .
So Pythagorus says-
3 2 + B E 2 = 2 4 2
⇒ B E = 5 6 7
⇒ ( b − 3 ) 2 + 5 6 7 = a 2
Also according to Circle Power of a Point Theorum , b ( b − 3 ) = a ( a − 1 )
By solving the above two equations, we get a + b = 2 8 7 . 4 9 6
So we get the perimeter 3 1 1 . 4 9 6 ≈ 3 1 1
Angles AEB and BFA are inscribed in a semicircle and hence 90° cos A = 2 4 3 ; cos B = 2 4 1 sin A = 2 4 5 6 7 ; sin B = 2 4 5 7 5 Get sin C using
sin C = (180° - A - B) = sin (A+B) = sin A. cos B + cos A. sin B sin C = 2 4 2 5 6 7 + 3 5 7 5 Then use sine rule to get C B = sin C 2 4 sin A = 5 6 7 + 3 5 7 5 2 4 2 5 6 7 C A = sin C 2 4 sin B = 5 6 7 + 3 5 7 5 2 4 2 5 7 5 Add CB + BA + AC to get 3 1 1 . 4 9 6 5